题目内容
14．若m=$\sqrt{5}$+1，则m+$\frac{1}{m}$=$\frac{5\sqrt{5}+3}{4}$．分析 先把m的值代入m+$\frac{1}{m}$，再进行分母有理化，然后合并即可．
解答 解：∵m=$\sqrt{5}$+1，
∴m+$\frac{1}{m}$=$\sqrt{5}$+1+$\frac{1}{\sqrt{5}+1}$
=$\sqrt{5}$+1+$\frac{\sqrt{5}-1}{4}$
=$\frac{5\sqrt{5}+3}{4}$．
故答案为=$\frac{5\sqrt{5}+3}{4}$．
点评 本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．二次根式运算的最后，注意结果要化到最简二次根式，二次根式的乘除运算要与加减运算区分，避免互相干扰．
练习册系列答案
相关题目
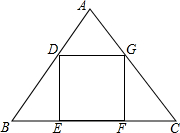如图，在△ABC中，AB=AC，正方形DEFG的顶点D、G分别在AB、AC上，EF在BC上，设AB=5，BC=6，求正方形DEFG的边长．