题目内容
10. 如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
分析 根据BE=CF,求出BC=EF,根据AAS推出△ABC≌△DEF,根据全等三角形的性质推出即可.
解答 证明:∵BE=CF(已知),
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(AAS),
∴AC=DF(全等三角形对应边相等).
点评 本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $\sqrt{12}÷\sqrt{3}$=2 | C. | ($\sqrt{5}$)-1=$\sqrt{5}$ | D. | ($\sqrt{3}$-1)2=2 |
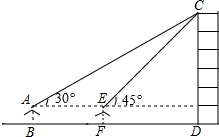 小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数) 高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示. 甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,当然取法各种各样.
甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,当然取法各种各样.