题目内容
15. 已知:如图所示,AC⊥AB于点A,BD⊥AB于点B,∠1=∠2,试判断AE与BF的位置关系,并说明理由.
已知:如图所示,AC⊥AB于点A,BD⊥AB于点B,∠1=∠2,试判断AE与BF的位置关系,并说明理由.
分析 根据垂直的定义得出等角的余角相等,再利用平行线的判定解答即可.
解答 解:AE∥BF.理由如下:
∵AC⊥AB,(已知)
∴∠CAB=90°,(垂直的定义)
即∠1+∠3=90°,
同理,∠2+∠4=90°,
∵∠1=∠2,(已知)
∴∠3=∠4,(等角的余角相等)
∴AE∥BF.(同位角相等,两直线平行)
点评 此题考查平行线的判定,关键是利用等角的余角相等和平行线的判定方法.

练习册系列答案
相关题目
20.下列计算中,正确的是( )
| A. | 2a2+3a2=5a4 | B. | (a-b)2=a2-b2 | C. | (a3)3=a6 | D. | (-2a2)3=-8a6 |
3. 如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
 如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
10.在第二象限内,到x轴距离为3,到y轴距离为2的点P坐标为( )
| A. | (3,2) | B. | (2,3) | C. | (-3,2) | D. | (-2,3) |
5.计算(2a2)3的结果是( )
| A. | 2a5 | B. | 2a6 | C. | 6a6 | D. | 8a6 |
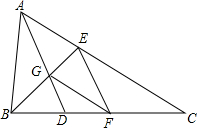 如图,在△ABC中,点D、E分别在边BC、AC上,BE、AD相交于点G,EF∥AD交BC于点F,且BF2=BD•BC,联结FG.
如图,在△ABC中,点D、E分别在边BC、AC上,BE、AD相交于点G,EF∥AD交BC于点F,且BF2=BD•BC,联结FG.