题目内容
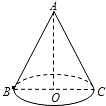 如图,圆锥的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是
如图,圆锥的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:首先求出圆锥侧面展开图的圆心角,进而得出B到AC的最短距离.
解答: 解:如图所示:
解:如图所示:
∵圆锥的底面直径BC=4cm,
∴圆锥的底面圆的周长为:4πcm,
圆锥侧面展开图的扇形弧长为:4π=
,
解得:n=120,
故∠BAC=60°,AC⊥BB′,
则∠ABD=30°,
∵AB=6cm,
∴AD=3cm,则BD=3
(cm),
故由点B出发,经过圆锥的侧面到达母线AC的最短路程是3
cm.
故答案为:3
cm.
 解:如图所示:
解:如图所示:∵圆锥的底面直径BC=4cm,
∴圆锥的底面圆的周长为:4πcm,
圆锥侧面展开图的扇形弧长为:4π=
| nπ×6 |
| 180 |
解得:n=120,
故∠BAC=60°,AC⊥BB′,
则∠ABD=30°,
∵AB=6cm,
∴AD=3cm,则BD=3
| 3 |
故由点B出发,经过圆锥的侧面到达母线AC的最短路程是3
| 3 |
故答案为:3
| 3 |
点评:此题主要考查了侧面展开图最短路径问题,求出扇形圆心角是解题关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
大于-3小于5的所有整数的积是( )
| A、240 | B、-240 |
| C、0 | D、-3600 |
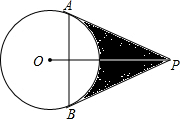 如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
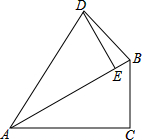 将Rt△ABC绕点A逆时针旋转40度,得到Rt△ADE,点E恰好落在斜边AB上,连接BD,则∠BDE=
将Rt△ABC绕点A逆时针旋转40度,得到Rt△ADE,点E恰好落在斜边AB上,连接BD,则∠BDE=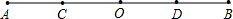 如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想:
如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想: 如图,以O为顶点的两条抛物线分别经过正方形的四个顶点A、B、C、D,则阴影部分的面积为
如图,以O为顶点的两条抛物线分别经过正方形的四个顶点A、B、C、D,则阴影部分的面积为 △ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;
△ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;