题目内容
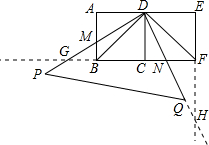 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板的直角顶点放置在D点处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板的直角顶点放置在D点处,DP交AB于点M,DQ交BF于点N.(1)求证:△DBM≌△DFN;
(2)延长正方形的边CB和EF,分别与直角三角板的两边DP、DQ(或它们的延长线)交于点G和点H,试探究下列问题:
①线段BG与FH相等吗?说明理由;
②当线段FN的长是方程x2+2x-3=0的一根时,试求出
| NG |
| NH |
考点:四边形综合题
专题:
分析:(1)如图1,根据正方形的性质就可得出BD=FD,∠ADB=∠CDF=∠ADB=∠CFD=45°,由直角三角形的性质就可以得出∠1=∠ADM,进而得出∠3=∠4,由ASA就可以得出结论;
(2)①如图1,根据正方形的性质及直角三角形的性质就可以得出△GCD≌△HED就有CG=EH,由等式的性质就可以得出结论;
②先解方程x2+2x-3=0就可以求出FN=1,得出CN=1,如图2,就可以得出△CND≌△FNH,得出CD=FH=2,就可以得出GB=2,GN=5,由勾股定理就可以求出NH的值,进而得出结论.
(2)①如图1,根据正方形的性质及直角三角形的性质就可以得出△GCD≌△HED就有CG=EH,由等式的性质就可以得出结论;
②先解方程x2+2x-3=0就可以求出FN=1,得出CN=1,如图2,就可以得出△CND≌△FNH,得出CD=FH=2,就可以得出GB=2,GN=5,由勾股定理就可以求出NH的值,进而得出结论.
解答:解:(1)如图1,∵四边形形ABCD和四边形CDEF是边长正方形,
∴BC=FC,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠E=∠HFN=∠ADC=90°.
∴∠ADM+∠CDM=90°,
∵∠PDQ=90°,
∴∠CDM+∠CDN=90°.
∴∠ADM=∠CDN.
∴∠ADB-∠ADM=∠CDF-∠CDN,
∴∠MDB=∠NDF.
在△DBM和△DFN中,
,
∴△DBM≌△DFN(ASA);
(2)①形形ABCD和四边形CDEF是边长正方形,
∴BC=FC=EF,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠CDE=∠E=∠HFN=∠ADC=90°.
∴∠EDH+∠1=90°,
∵∠PDQ=90°,
∴∠CDM+∠1=90°.
∴∠CDM=∠EDH.
在△CDG和△EDH中,
,
∴△CDG≌△EDH(ASA),
∴CG=EH,
∴CG-CB=EH-EF,
∴BG=FH.
②∵x2+2x-3=0,
∴x1=1,x2=-3.
∵FN的长是方程x2+2x-3=0的一根,
∴FN=1.
∴CN=1,
∴CN=FN.
在△CND和△FNH中,
,
∴△CND≌△FNH(ASA),
∴CD=FH=2,
∴GB=2,
∴GN=5.
在Rt△FNH中,由勾股定理,得NH=
.
∴
=
=
.
∴BC=FC,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠E=∠HFN=∠ADC=90°.

∴∠ADM+∠CDM=90°,
∵∠PDQ=90°,
∴∠CDM+∠CDN=90°.
∴∠ADM=∠CDN.
∴∠ADB-∠ADM=∠CDF-∠CDN,
∴∠MDB=∠NDF.
在△DBM和△DFN中,
|
∴△DBM≌△DFN(ASA);
(2)①形形ABCD和四边形CDEF是边长正方形,
∴BC=FC=EF,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠CDE=∠E=∠HFN=∠ADC=90°.
∴∠EDH+∠1=90°,
∵∠PDQ=90°,
∴∠CDM+∠1=90°.
∴∠CDM=∠EDH.
在△CDG和△EDH中,
|
∴△CDG≌△EDH(ASA),
∴CG=EH,
∴CG-CB=EH-EF,
∴BG=FH.
②∵x2+2x-3=0,
∴x1=1,x2=-3.
∵FN的长是方程x2+2x-3=0的一根,
∴FN=1.

∴CN=1,
∴CN=FN.
在△CND和△FNH中,
|
∴△CND≌△FNH(ASA),
∴CD=FH=2,
∴GB=2,
∴GN=5.
在Rt△FNH中,由勾股定理,得NH=
| 5 |
∴
| NG |
| NH |
| 5 | ||
|
| 5 |
点评:本题考查了正方形的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等式的性质的运用,解答时证明三角形全等灵活运用全等三角形的性质是关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.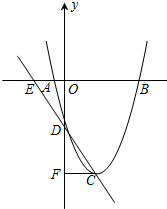 已知抛物线y=
已知抛物线y=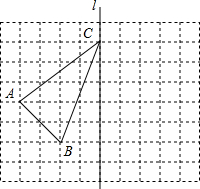 如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.
如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上. 在△ABC中,∠A=60°,∠ABC、∠ACB所对的b、c满足:b2+c2-2(b+c)+2=0.
在△ABC中,∠A=60°,∠ABC、∠ACB所对的b、c满足:b2+c2-2(b+c)+2=0.