题目内容
探究题:对于正数a和b,有下列命题:
若
=1,则a+b≥2;若
=
,则a+b≥3;
若
=2,则a+b≥4;若
=
,则a+b≥5.
根据以上四个命题的规律猜想:
①若
=5,则a+b≥ ;
②对于任意正数x、y,存在的规律可以表示为 .
若
| ab |
| ab |
| 3 |
| 2 |
若
| ab |
| ab |
| 5 |
| 2 |
根据以上四个命题的规律猜想:
①若
| ab |
②对于任意正数x、y,存在的规律可以表示为
考点:命题与定理
专题:规律型
分析:①根据a+b≥2
即可得出答案;
②把存在的规律用公式表示出来即可.
| ab |
②把存在的规律用公式表示出来即可.
解答:解:①若
=5,则a+b≥10
②对于任意正数x、y,存在的规律可以表示为:x+y≥2
(x>0,y>0),
故答案为:10,x+y≥2
(x>0,y>0).
| ab |
②对于任意正数x、y,存在的规律可以表示为:x+y≥2
| xy |
故答案为:10,x+y≥2
| xy |
点评:此题考查了命题与定理,关键是通过观察例子得出存在的规律x+y≥2
(x>0,y>0),注意x、y的取值范围.
| xy |

练习册系列答案
相关题目

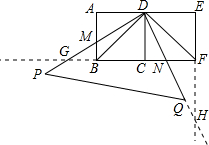 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板的直角顶点放置在D点处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板的直角顶点放置在D点处,DP交AB于点M,DQ交BF于点N.
 如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为
如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为