题目内容
把正整数1,2,3,4,5,…,按如下规律排列:

(1)按此规律,可知第n行有 个正整数. 第20行的第一个和最后一个数分别是 、 ;
(2)第n行的最后一个数是 .

(1)按此规律,可知第n行有
(2)第n行的最后一个数是
考点:规律型:数字的变化类
专题:
分析:(1)第一行有1个正整数,第二行有2个正整数,…第n行有n个正整数,每行第一个数为1+1+2+3+…+(n-1)=1+
;最后一个数是1+2+3+…+n=
;由此求得答案即可;
(2)利用(1)中的规律直接得出.
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
(2)利用(1)中的规律直接得出.
解答:解:(1)第一行有1个正整数,
第二行有2个正整数,
…
第n行有n个正整数;
第一行的第一个数为1,最后一个数为1,
第二行的第一个数为2=1+1,最后一个数为3=1+2,
第三行的第一个数为4=1+1+2,最后一个数为6=1+2+3,
第四行的第一个数为7=1+1+2+3,最后一个数为10=1+2+3+4,
…
每n行第一个数为1+1+2+3+…+(n-1)=1+
;最后一个数是1+2+3+…+n=
;
所以第n行有n个正整数. 第20行的第一个和最后一个数分别是191、210.
(2)第n行的最后一个数是
.
故答案为:(1)n,191、210;(2)是
.
第二行有2个正整数,
…
第n行有n个正整数;
第一行的第一个数为1,最后一个数为1,
第二行的第一个数为2=1+1,最后一个数为3=1+2,
第三行的第一个数为4=1+1+2,最后一个数为6=1+2+3,
第四行的第一个数为7=1+1+2+3,最后一个数为10=1+2+3+4,
…
每n行第一个数为1+1+2+3+…+(n-1)=1+
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
所以第n行有n个正整数. 第20行的第一个和最后一个数分别是191、210.
(2)第n行的最后一个数是
| n(n+1) |
| 2 |
故答案为:(1)n,191、210;(2)是
| n(n+1) |
| 2 |
点评:此题考查数字的变化规律,注意结合数的排列形状,找出规律解决问题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
能将两直角边长分别为6和8的直角三角形完全覆盖的最小圆面积为( )
| A、100π | B、50π |
| C、25π | D、16π |
 已知如图,△ABC≌△DCB,其中的:
已知如图,△ABC≌△DCB,其中的: 如图,∠ACB=90°,E、F为AB上的点,AE=AC,BC=BF,则∠ECF=
如图,∠ACB=90°,E、F为AB上的点,AE=AC,BC=BF,则∠ECF=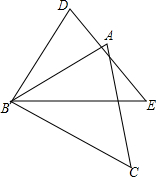 如图,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件
如图,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件