题目内容
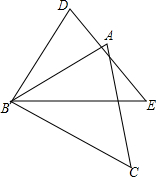 如图,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件
如图,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件考点:全等三角形的判定
专题:开放型
分析:根据∠ABD=∠CBE,可得∠ABD+∠ABE=∠CBE+∠ABE,即可得出∠DBE=∠ABC,只需添加BE=BC,便可根据SAS判定△ABC≌△DBE.
解答:解:添加条件:BC=BE.
∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠DBE=∠ABC,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS).
故答案为:BC=BE.
∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠DBE=∠ABC,
在△ABC和△DBE中,
|
∴△ABC≌△DBE(SAS).
故答案为:BC=BE.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
如果二次函数y=ax2+bx+c中,a:b:c=2:3:4,且这个函数的最小值为
,则这个二次函数为( )
| 23 |
| 4 |
| A、y=2x2+3x+4 |
| B、y=4x2+6x+8 |
| C、y=4x2+3x+2 |
| D、y=8x2+6x+4 |
下列运算正确的( )
| A、a3-a2=a |
| B、a2•a3=a6 |
| C、(a3)2=a6 |
| D、(3a)3=9a3 |
 如图,已知△ABC,AB>AC,利用直尺与圆规作一点P(保留作图痕迹),使得PA=PB=PC,并说明理由.
如图,已知△ABC,AB>AC,利用直尺与圆规作一点P(保留作图痕迹),使得PA=PB=PC,并说明理由.