题目内容
14.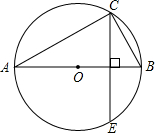 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,弦CE⊥AB于D,已知sinA=$\frac{3}{5}$,BC=4,则CE的长为$\frac{32}{5}$.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,弦CE⊥AB于D,已知sinA=$\frac{3}{5}$,BC=4,则CE的长为$\frac{32}{5}$.
分析 如图,首先运用圆周角定理、锐角函数的定义求出AB的长度;其次运用勾股定理求出AC的长度;借助三角形的面积公式求出CD的长度,即可解决问题.
解答 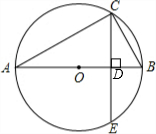 解:如图,∵AB为⊙O的直径,
解:如图,∵AB为⊙O的直径,
∴∠ACB=90°,
∴sin∠A=$\frac{BC}{AB}=\frac{3}{5}$,而BC=4,
∴AB=$\frac{20}{3}$;由勾股定理得:
AC2=AB2-BC2,
解得:AC=$\frac{16}{3}$;
∵弦CE⊥AB于D,
∴CD=DE;由三角形的面积公式得:
$\frac{1}{2}AC•BC=\frac{1}{2}AB•CD$,
解得:CD=$\frac{16}{5}$,
∴CE=2CD=$\frac{32}{5}$,
故答案为$\frac{32}{5}$.
点评 该题主要考查了垂径定理、圆周角定理、锐角三角函数的定义等几何知识点及其应用问题;牢固掌握垂径定理、圆周角定理等几何知识点是基础,灵活运用是关键.

练习册系列答案
相关题目
19.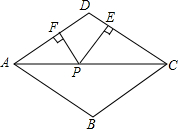 如图,P为菱形ABCD的对角线AC上一点,AB=2cm,∠B=120°,PE⊥CD于点E,PF⊥AD于点F,则PE+PF的值为( )
如图,P为菱形ABCD的对角线AC上一点,AB=2cm,∠B=120°,PE⊥CD于点E,PF⊥AD于点F,则PE+PF的值为( )
 如图,P为菱形ABCD的对角线AC上一点,AB=2cm,∠B=120°,PE⊥CD于点E,PF⊥AD于点F,则PE+PF的值为( )
如图,P为菱形ABCD的对角线AC上一点,AB=2cm,∠B=120°,PE⊥CD于点E,PF⊥AD于点F,则PE+PF的值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{3\sqrt{2}}{2}$ |
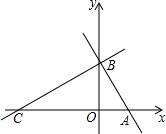 如图,在平面直角坐标系中,已知A(1,0),∠ABO=∠BCO=30°
如图,在平面直角坐标系中,已知A(1,0),∠ABO=∠BCO=30° 如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明:∠FGA=∠ACB.
如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明:∠FGA=∠ACB.