题目内容
11.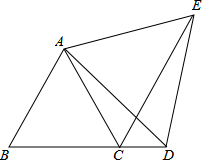 如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,
如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:
(1)△ABD≌△ACE;
(2)△ADE为等边三角形.
分析 (1)根据等边三角形的性质得出AB=AC,∠BAC=∠B=∠ACB=60°,求出∠ACE=∠B,根据SAS推出全等即可;
(2)根据全等三角形的性质得出AD=AE,∠CAE=∠BAD,求出∠DAE=∠BAC=60°,根据等边三角形的性质得出即可.
解答 证明:(1)∵△ABC等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=60°,
∴∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=$\frac{1}{2}$∠ACD=60°,
∴∠ACE=∠B,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACE}\\{BD=CE}\end{array}\right.$
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴AD=AE,∠CAE=∠BAD,
∴∠DAE=∠BAC=60°,
∴△ADE为等边三角形.
点评 本题考查了等边三角形的性质和判定,全等三角形的性质和判定的应用,能推出△ABD≌△ACE是解此题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
19.在数轴上,把-2的对应点向右移动4个单位后,所得的对应点表示的数是( )
| A. | -2 | B. | -6 | C. | 2 | D. | 2或-6 |
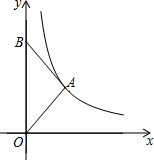 如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.
如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.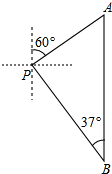 如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,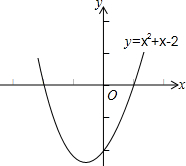 观察函数的图象.完成填空;
观察函数的图象.完成填空;