Question

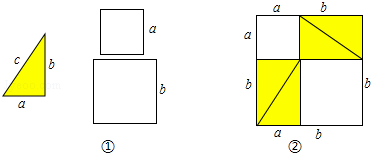
11．如图①是1个直角三角形和2个小正方形，直角三角形的三条边长分别是a、b、c，其中a、b是直角边．正方形的边长分别是a、b．
（1）将4个完全一样的直角三角形和2个小正方形构成一个大正方形（如图②）．用两种不同的方法列代数式表示图②中的大正方形面积：
方法一：（a+b）²；       方法二：a²+2ab+b²；
（2）观察图②，试写出（a+b）²，a²，2ab，b²这四个代数式之间的等量关系；
（3）请利用（2）中等量关系解决问题：
已知图①中一个三角形面积是6，图②的大正方形面积是49，求a²+b²的值．
（4）利用你发现的结论，求：997²+6×997+3²的值．

Answer 1

分析 （1）利用两种方法表示出大正方形面积即可；
（2）写出四个代数式之间的等量关系即可；
（3）利用得出的结果把原式变形，计算即可得到结果．
（4）利用完全平方公式进行解答即可．

解答 解：（1）方法一：（a+b）²；    
方法二：a²+2ab+b²；        
故答案为：（a+b）²；a²+2ab+b²；
（2）（a+b）²=a²+2ab+b²； 
（3）a²+b²=（a+b）²-2ab                    
=49-4×6
=25．                                               
（4）997²+6×997+3²
=997²+2×997×3+3²
=（997+3）²
=1000²
=1000000．

点评 此题考查了代数式求值，以及列代数式，熟练掌握运算法则是解本题的关键．