题目内容
3. 如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(4,0),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC中点,则k的值是3$\sqrt{3}$.
如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(4,0),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC中点,则k的值是3$\sqrt{3}$.
分析 设BC中点为D,过C作CE⊥AB于E,过D作DF⊥AB于F,由△ABC是等边三角形,得到AC=AB=4,∠CAB=∠ABC=60°,求出CE=2$\sqrt{3}$,AE=BE=2,根据三角形的中位线定理得到D(3,$\sqrt{3}$),即可求得结果.
解答  解:设BC中点为D,过C作CE⊥AB于E,过D作DF⊥AB于F,
解:设BC中点为D,过C作CE⊥AB于E,过D作DF⊥AB于F,
∵△ABC是等边三角形,
∴AC=AB=4,∠CAB=∠ABC=60°,
∴CE=2$\sqrt{3}$,AE=BE=2,
∵CE⊥AB,DF⊥AB,
∴CE∥DF,
∵CD=BD,
∴BF=EF=1,
∴D(3,$\sqrt{3}$),
∵点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=3$\sqrt{3}$,
故答案为:3$\sqrt{3}$.
点评 本题考查了确定反比例函数y=$\frac{k}{x}$(k≠0)的k值的方法:通过几何方法得到其图象上某点的横纵坐标之积即可.也考查了等腰三角形的性质以及三角形中位线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.方程3-2(x-5)=9的解是( )
| A. | x=-2 | B. | x=2 | C. | x=$\frac{2}{3}$ | D. | x=1 |
14.和-2的相反数相等的是( )
| A. | -2的平方 | B. | -2的倒数 | C. | -2的绝对值 | D. | 4的平方根 |
18.计算:(-a)3•a2正确的结果是( )
| A. | -a5 | B. | a5 | C. | -a6 | D. | a6 |
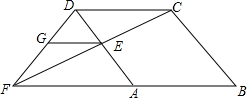 如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.
如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.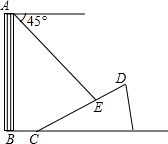 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.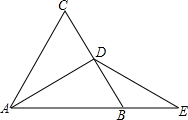 如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.
如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD. 如图,在?ABCD中,AD=2AB,E,F在直线AB上,CE与AD交于点M,DF与CB交于点N,且AE=AB=BF.
如图,在?ABCD中,AD=2AB,E,F在直线AB上,CE与AD交于点M,DF与CB交于点N,且AE=AB=BF.