题目内容
11．设方程x2-（a+10）x+10a-1=0有两个整数根，则整数a=10．分析 先计算判别式得到△=（a-10）2+4，然后利用方程有两个整数根得到（a-10）2=0，从而可得到a的值．
解答 解：∴△=（a+10）2-4（10a-1）=（a-10）2+4，
∴方程有两个整数根，
∴△为完全平方式，
∴（a-10）2=0，
∴a=10．
故答案为10．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
互动英语系列答案
相关题目
1．a、b是两个连续整数，若a＜$\sqrt{3}$＜b，则a、b分别是（ ）
| A． | 0、1 | B． | 1、2 | C． | 2、3 | D． | 3、4 |
2．已知P1（x1，y1），P2（x2，y2）是一次函数y=-$\frac{1}{3}$x+2图象上的两点，下列判断中，正确的是（ ）
| A． | y1＞y2 | B． | y1＜y2 | C． | 当x1＜x2时，y1＜y2 | D． | 当x1＜x2时，y1＞y2 |
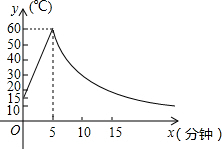制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
如图，△ABC中，∠C=60°，点M是AC中点，点G是△ABC的重心，CD⊥BC于点D，若GD=4cm，则AC=6$\sqrt{3}$．
16．下列二次分式中，与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{\frac{1}{2}}$ | B． | $\sqrt{4}$ | C． | $\sqrt{12}$ | D． | $\sqrt{24}$ |
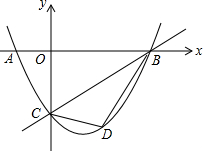如图，直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴交于点B，与y轴交于点C，抛物线y=ax2+bx-$\sqrt{3}$经过点A、B、C，且点A坐标是（-1，0），点D是直线BC下方抛物线上的一动点．