题目内容
6. 如图,△ABC中,∠C=60°,点M是AC中点,点G是△ABC的重心,CD⊥BC于点D,若GD=4cm,则AC=6$\sqrt{3}$.
如图,△ABC中,∠C=60°,点M是AC中点,点G是△ABC的重心,CD⊥BC于点D,若GD=4cm,则AC=6$\sqrt{3}$.
分析 作MN⊥BC于N,根据重心的概念得到BG=2GM,根据相似三角形的性质求出MN,根据正弦的概念计算即可.
解答 解: 作MN⊥BC于N,
作MN⊥BC于N,
则GD∥MN,
∵点G是△ABC的重心,
∴BG=2GM,
∵GD∥MN,
∴$\frac{DG}{MN}$=$\frac{BD}{BM}$=$\frac{2}{3}$,
∴MN=6,
∵∠C=60°,
∴MC=$\frac{MN}{sin∠C}$=3$\sqrt{3}$,
∴AC=2MC=6$\sqrt{3}$,
故答案为:6$\sqrt{3}$.
点评 本题考查的是三角形的重心的概念和性质、平行线的性质以及锐角三角函数的应用,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.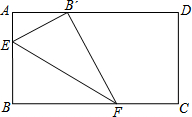 如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
 如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 5$\sqrt{5}$ | D. | 10 |
1.3月7日,在百度中输入“世界关注中国两会”,得到相关结果约有 2040000个,将2040000用科学记数法表示是( )
| A. | 2.04×106 | B. | 2.04×105 | C. | 2.04×104 | D. | 204×104 |
18.某居民小区开展节约用水活动,3月份各户用水量比2月份有所下降,不同节水量的户数统计如下表所示:
那么3月份平均每户节水量是( )
| 节水量(立方米) | 1 | 2 | 3 |
| 户数 | 20 | 120 | 60 |
| A. | 1.9立方米 | B. | 2.2立方米 | C. | 33.33立方米 | D. | 66.67立方米 |
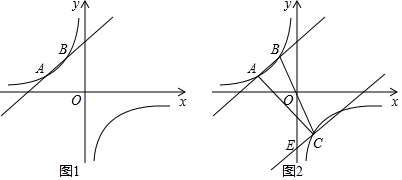
 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限,直线y=x+1交y轴于点D,且点D为CO中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为($\sqrt{3}$,2).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限,直线y=x+1交y轴于点D,且点D为CO中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为($\sqrt{3}$,2).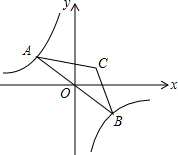 如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.
如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.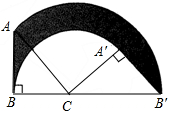 如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.
如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.