题目内容
3．若一次函数y=（m-1）x+m2-1的图象通过原点，则m的值为（ ）| A． | m=-1 | B． | m=1 | C． | m=±1 | D． | m≠1 |
分析 根据一次函数的定义及函数图象经过原点的特点列出关于m的不等式组，求出m的值即可．
解答 解：∵一次函数y=（m-1）x+m2-1的图象经过原点，
∴0=0+m2-1，m-1≠0，即m2=1，m≠1
解得，m=-1．
故选A．
点评 本题考查的是一次函数图象上点的坐标特点，即一次函数y=kx+b（k≠0）中，当b=0时函数图象经过原点．．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，求EF的长．
18．已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且0＜y-x＜1，则k的取值范围是（ ）
| A． | -1$＜k＜-\frac{1}{2}$ | B． | 0$＜k＜\frac{1}{2}$ | C． | 0＜k＜1 | D． | $\frac{1}{2}$＜k＜1 |
8．已知直角三角形的两边长分别为6和8，则这个直角三角形的周长是（ ）
| A． | 24或14+2$\sqrt{7}$ | B． | 24 | C． | 20或14-2$\sqrt{7}$ | D． | 22或14+2$\sqrt{7}$ |
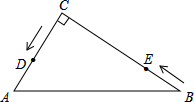如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s的速度沿折线C→A→B向点B运动，同时，点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为ts（0＜t＜8）．