题目内容
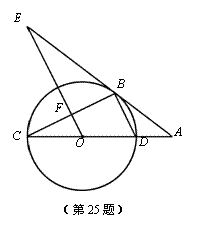
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:∠E=∠BCO;
(2)若⊙O的半径为3,cosA=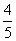 ,求EF的长.
,求EF的长.
 |
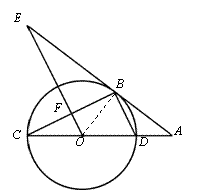 (1)证明:连接BO.
(1)证明:连接BO.
∵OE∥BD,
∴∠E=∠ABD.
∵AE与⊙O相切于点B,∴OB⊥AE.
∴∠ABD+∠OBD=90°.
∵CD是⊙O的直径,
∴∠CBO+∠OBD=90°.
∴∠ABD=∠CBO.
∵OB=OC,
∴∠CBO=∠BCO.
∴∠E=∠BCO. 4分
(2)解:在Rt△ABO中,cosA=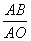 =
=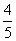 ,可设AB=4k,AO=5k,
,可设AB=4k,AO=5k,
BO=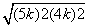 =3k.
=3k.
∵⊙O的半径为3,∴3k=3,∴k=1.
∴AB=4,AO=5.
∴AD=AO-OD=5-3=2.
∵BD∥EO,
∴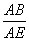 =
=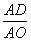 =
=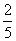 ,∴AE=10.
,∴AE=10.
∴EB=AE-AB=6.
在Rt△EBO中,EO=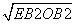 =3
=3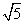 .
.
∵OE∥BD,
∴∠EFB=∠DBF=90°.
∵∠FEB=∠BEO,∠EFB=∠EBO,
∴△EFB∽△EBO.
∴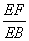 =
=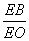 ,即
,即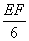 =
=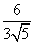 .
.
∴EF=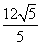 . 9分
. 9分

(1)已知:如图,E、F、G、H分别是菱形ABCD的各边上与顶点均不重合的点,且AE=CF=CG=AH.
求证:四边形EFGH是矩形.
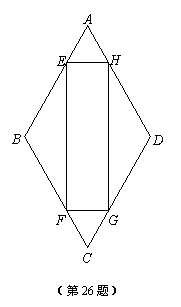 |
(2)已知: E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的点,且四边形EFGH是矩形.AE与AH相等吗?如果相等,请说明理由;如果不相等,请举反例进行说明.
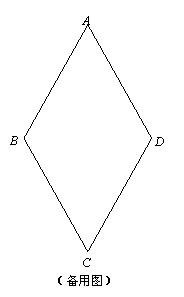 |

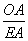 = .
= .

 有意义的x的取值范围是
有意义的x的取值范围是 -
- )×
)× 的结果是 .
的结果是 . 的圆中,60°的圆心角所对的弧等于
的圆中,60°的圆心角所对的弧等于