题目内容
在一个不透明的口袋里装有四个球,这四个球上分别标记数字-3、-1、0、2,除数字不同外,这四个球没有任何区别.
(1)从中任取一球,求该球上标记的数字为正数的概率;
(2)从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.
解:(1)正数为2,该球上标记的数字为正数的概率为 . 3分
. 3分
(2)点(x,y)所有可能出现的结果有:
(-3,-1)、(-3,0)、(-3,2)、(-1,0)、(-1,2)、(0,2)、
(-1,-3)、(0,-3)、(2,-3)、(0,-1)、(2,-1)、(2,0).
共有12种,它们出现的可能性相同.所有的结果中,
满足“点(x,y)位于第二象限”(记为事件A)的结果有2种,所以P(A)=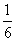 . 8分
. 8分

 学业测评一课一测系列答案
学业测评一课一测系列答案某纪念币从2013年11月11日起开始上市,通过市场调查得知该纪念币每1枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
(1)根据上表数据,在某一特定时期内,可从下列函数中选取一个恰当的函数描述纪念币的市场价y与上市时间x的变化关系:
① y=ax+b(a≠0); ② y=a(x-h)2+k( a≠0); ③ y=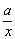 (a≠0).
(a≠0).
你可选择的函数的序号是 .
(2)利用你选取的函数,求该纪念币上市多少天时市场价最低,最低价格是多少?
 .
.

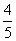 ,求EF的长.
,求EF的长.