题目内容
10.已知四边形ABCD,AD∥BC,∠D=90°,∠BAD=120°,AC平分∠BAD,AB=2AD.(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点E在BA的延长线上,在BC取一点F,连接EC,EF,且EC=EF,求证:BF=AE.
(3)连接AF,取CE的中点M,作MH⊥AF,探究MH⊥AF,探究:FH、AH之间的数量关系,并证明你的结论.
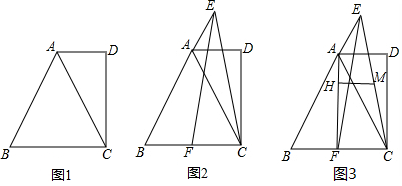
分析 (1)只要证明∠B=∠BCA=∠BAC=60°即可.
(2)如图2中,作FM∥AC交AB于M.首先证明△BFM是等边三角形,再证明△EMF≌△CAE即可解决问题.
(3)如图3中,连接AM、FM,在AB上截取AN=BF,连接CN交AF于K,在AF上截取AG=AM,连接GM.只要证明△AMF是含有60°的直角三角形即可解决问题.
解答 (1)证明:如图1中,
∵∠BAD=120°,AC平分∠BAD,
∴∠CAB=∠CAD=60°,
∵AD∥BC,
∴∠DAC=∠BCA=60°,
∴∠B=∠BCA=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:如图2中,作FM∥AC交AB于M.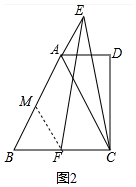
∵MF∥AC,
∴∠BMF=∠BAC=60°,∠BFM=∠BCA=60°,
∴∠B=∠BMF=∠BFM=60°,
∴△BMF是等边三角形,
∴FM=BF,∠EMF=120°=∠EAC,
∵EF=EC,
∴∠EFC=∠ECF,
∴∠EFM=180°-60°-∠EFC=120°-∠EFC,∠AEC=180°-60°-∠ECB=120°-∠ECF,
∴∠MFE=∠AEC,
∴△EMF≌△CAE,
∴AE=FM=BF,
∴AE=BF.
(3)结论:FH=3AH.
理由:如图3中,连接AM、FM,在AB上截取AN=BF,连接CN交AF于K,在AF上截取AG=AM,连接GM.
∵AN=BF,AC=AB,∠ABF=∠CAN,
∴△ABF≌△CAN,
∴∠BAF=∠ACN,AF=NC,
∴∠AKN=∠CAK+∠ACN=∠CAK+∠BAF=60°,
∵AE=BF=AN,EM=MC,
∴AM∥NC,AM=$\frac{1}{2}$NC=$\frac{1}{2}$AF,
∴∠FAM=∠AKN=60°,∵AG=AM,
∴△AGM是等边三角形,
∴AG=GM=AM=$\frac{1}{2}$AF,∠AGM=∠AMG=60°,
∴GM=GF,
∴∠GFM=∠GMF=30°,
∴∠AMF=∠AMG+∠GMF=90°,
∵MH⊥AF,
∴∠AHM=90°,∠AMH=30°,
∴AF=2AM,AM=2AH,
∴AF=4AH,
∴FH=3AH.
点评 本题考查四边形综合题、全等三角形的判定和性质、等边三角形的判定和性质、直角三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,善于用特殊图形思考问题,找到问题的突破口,善于中考压轴题.

| A. | 3,-2 | B. | 3,2 | C. | 3,5 | D. | 5,2 |
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
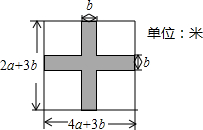 如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.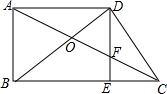 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F. 如图△ABC是等边三角形,BD平分∠ABC,延长BC至E,连结DE,此时DB=DE.求证:CE=CD.
如图△ABC是等边三角形,BD平分∠ABC,延长BC至E,连结DE,此时DB=DE.求证:CE=CD.