题目内容
(1)用乘法公式计算
①2003×2001
②(3a+2b-1)(3a-2b+1)
(2)根据x2+(a+b)x+ab=(x+a)(x+b),分解因式.
①x2-13x+36;
②x2-6ax-16a2.
(3)已知2x-3=0,求代数式x(x2-x)(5-x)-9的值.
①2003×2001
②(3a+2b-1)(3a-2b+1)
(2)根据x2+(a+b)x+ab=(x+a)(x+b),分解因式.
①x2-13x+36;
②x2-6ax-16a2.
(3)已知2x-3=0,求代数式x(x2-x)(5-x)-9的值.
考点:平方差公式,完全平方公式,因式分解-十字相乘法等
专题:
分析:(1)根据平方差公式,可得答案;
(2)根据十字相乘法,可得答案;
(3)根据代数式求值,可得答案.
(2)根据十字相乘法,可得答案;
(3)根据代数式求值,可得答案.
解答:解(1)①2003×2001=(2002+1)×(2002-1)=20022-1;
②原式=[3a+(2b-1)][3a-(2b-1)]=9a2-(2b-1)2=9a2-4b2+4b-1;
(2)①原式=(x-4)(x-9),
②原式=(x-8a)(x+2a);
(3)由2x-3=0,得x=
.
当x=
时,x(x2-x)(5-x)-9=
×[(
)2-
](5-
)-9=
-9=-
.
②原式=[3a+(2b-1)][3a-(2b-1)]=9a2-(2b-1)2=9a2-4b2+4b-1;
(2)①原式=(x-4)(x-9),
②原式=(x-8a)(x+2a);
(3)由2x-3=0,得x=
| 3 |
| 2 |
当x=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 63 |
| 16 |
| 81 |
| 16 |
点评:本题考查了平方差公式,凑成平方差公式的形式是解题关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )
如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )| A、11个 | B、12个 |
| C、13个 | D、14个 |
 如图,△ABC被平行光照射,CD⊥AB于D,AB在投影面上,则AC的投影是什么?CD与BC的投影呢?
如图,△ABC被平行光照射,CD⊥AB于D,AB在投影面上,则AC的投影是什么?CD与BC的投影呢? 如图所示,已知△ABC和△BDE均为等边三角形,且A、B、E三点共线,连接AD、CE,若∠BAD=39°,那么∠AEC=
如图所示,已知△ABC和△BDE均为等边三角形,且A、B、E三点共线,连接AD、CE,若∠BAD=39°,那么∠AEC= 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
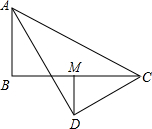 在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.
在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.