题目内容
10.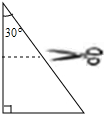 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
分析 如图1将△ABC沿EF剪下,可拼成矩形BCDE,由特殊锐角三角函数值可求得AB的长,然后根据矩形的周长2BC+2BE=2BC+AE即可得出答案;如图2将△ABC沿EF剪下,可拼成梯形DCFE,先求得AC的长,从而得到梯形的两腰之和,然后根据三角形的中位线定理可知EF=1,从而可求得梯形的上下底之和,故此可求得它的周长.
解答 解:如图1将△ABC沿EF剪下,可拼成矩形BCDE.
∵∠ABC=90°,∠A=30°,
∴$\frac{BC}{AB}=\frac{\sqrt{3}}{3}$,即$\frac{2}{AB}=\frac{\sqrt{3}}{3}$.
∴AB=2$\sqrt{3}$.
矩形BCDE的周长=2BC+2BE=2BC+AE=2×2+2$\sqrt{3}$=4+2$\sqrt{3}$;
如图2将△ABC沿EF剪下,可拼成梯形DCFE.
∵EF是三角形的中位线,
∴EF=$\frac{1}{2}BC=\frac{1}{2}×2=1$.
∴BD=1.
∵∠ABC=90°,∠A=30°,
∴AC=2CB=4.
∵DE=AF.
∴FC+DE=AC=4.
∴梯形四边形的周长=EF+BD+BC+FC+DE=1+1+2+4=8.
故答案为:8或4+2$\sqrt{3}$.
点评 本题主要考查的是图形的剪拼,根据题意画出剪拼后的图形是解题的关键.解答本题需要注意不要漏解.

练习册系列答案
相关题目
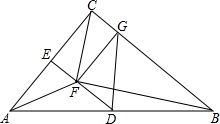 在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F是DE上一点,∠CBF=∠CAF,作FG⊥BC于点G,求证:
在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F是DE上一点,∠CBF=∠CAF,作FG⊥BC于点G,求证: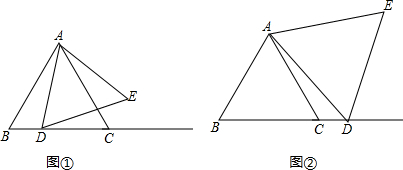
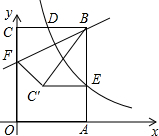 如图,直角坐标系中,矩形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴的正半轴上,若点B的坐标为(4,6),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,与AB交于点E,F为OC边上一点,把△BCF沿直线BF翻折,使点C落在点C′处(C′在矩形OABC内部),且C′E∥BC,则CF的长为$\frac{16-4\sqrt{7}}{3}$.
如图,直角坐标系中,矩形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴的正半轴上,若点B的坐标为(4,6),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,与AB交于点E,F为OC边上一点,把△BCF沿直线BF翻折,使点C落在点C′处(C′在矩形OABC内部),且C′E∥BC,则CF的长为$\frac{16-4\sqrt{7}}{3}$.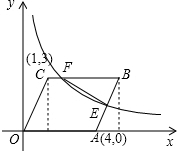 在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)
在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)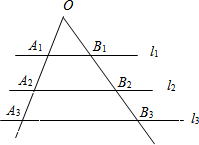 如图,一组平行线l1,l2,l3分别与∠O的两边相交于点A1,A2,A3和点B1,B2,B3,且梯形A1B1B2A2,A2B2B3A3的面积相等.设线段OA1=1,OA2=2,则线段A2A3=$\sqrt{7}$-2.
如图,一组平行线l1,l2,l3分别与∠O的两边相交于点A1,A2,A3和点B1,B2,B3,且梯形A1B1B2A2,A2B2B3A3的面积相等.设线段OA1=1,OA2=2,则线段A2A3=$\sqrt{7}$-2. 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度.
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度.