题目内容
7.下列各数中,不是无理数的是( )| A. | $\sqrt{2}$ | B. | π | C. | -$\frac{5}{6}$ | D. | $\root{3}{12}$ |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:A、$\sqrt{2}$是无理数,选项错误;
B、π是无理数,选项错误;
C、-$\frac{5}{6}$是分数,是有理数,不是无理数,选项正确;
D、$\root{3}{12}$是无理数,选项错误.
故选C.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B. | $\sqrt{8}$=4$\sqrt{2}$ | C. | $\sqrt{3}$•$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
2.下列命题中,是真命题的有( )
①同旁内角互补;
②若n<1,则n2-1<0;
③如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等;
④同一平面内,如果直线l1⊥l2,直线l2⊥l3,那么l1∥l3.
①同旁内角互补;
②若n<1,则n2-1<0;
③如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等;
④同一平面内,如果直线l1⊥l2,直线l2⊥l3,那么l1∥l3.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.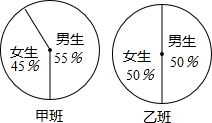 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )| A. | 58 | B. | 25 | C. | 27 | D. | 52 |
19.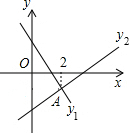 如图,直线y1=-x+m与y2=kx+n相交于点A,若点A的横坐标为2,则下列结论中错误的是( )
如图,直线y1=-x+m与y2=kx+n相交于点A,若点A的横坐标为2,则下列结论中错误的是( )
 如图,直线y1=-x+m与y2=kx+n相交于点A,若点A的横坐标为2,则下列结论中错误的是( )
如图,直线y1=-x+m与y2=kx+n相交于点A,若点A的横坐标为2,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
16.不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其他都相同)其中红球2个,黄球1个,蓝球1个,则搅匀后从中任意摸出一个球是红球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
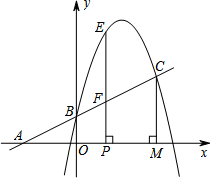 如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.
如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.