题目内容
11．
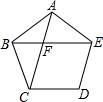如图，在正五边形ABCDE中，对角线AC、BE相交于点F，则F为线段BE的黄金分割点，若EF=2，则BE=$\sqrt{5}$+1．
分析 根据黄金比为$\frac{\sqrt{5}-1}{2}$进行计算即可得到答案．
解答 解：∵F为线段BE的黄金分割点，EF＞BE，
∴EF=$\frac{\sqrt{5}-1}{2}$BE，又EF=2，
∴BE=$\sqrt{5}$+1，
故答案为：$\sqrt{5}$+1．
点评 本题考查的是黄金分割的知识，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比．
练习册系列答案
优学名师名题系列答案
相关题目
1．下列调查中，适宜采用全面调查方式的是（ ）
| A． | 旅客上飞机前的安全检查 | |
| B． | 对广州市七年级学生身高现状的调查 | |
| C． | 多某品牌食品安全的调查 | |
| D． | 对一批灯管使用寿命的调查 |
19．下列图案中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
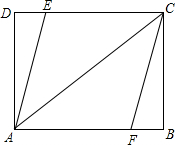如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．
16．
如图所示的几何体的俯视图是（ ）
如图所示的几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
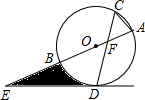如图，⊙O的直径AB与弦CD相交于点F，且∠ACD=60°，在AB的延长线上取一点E，使得∠AED=30°．