题目内容
19.某网店以每件40元的价格购进一款童装.由试销知,每星期的销售量t(件)与每件的销售价x(元)之间的函数关系式为t=-30x+2100.(1)求每星期销售这款童装的毛利润y(元)与每件销售价x(元)之间的函数表达式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)为了使每星期利润不少于6000元,求每件销售价x的取值范围.
分析 (1)根据总利润=(每件售价-40)×销售数量即可得出y关于x的函数表达式;
(2)利用配方法将(1)得出的函数表达式变形,再根据二次函数的性质即可解决最值问题;
(3)根据(1)结合每星期利润不少于6000元,即可得出关于x的一元二次不等式,解之即可得出每件销售价x的取值范围.
解答 解:(1)根据题意得:y=(x-40)t=(x-40)(-30x+2100)=-30x2+3300x-84000;
(2)y=-30x2+3300x-84000=-30(x-55)2+6750,
∵a=-30<0,
∴当x=55时,y取最大值,最大值为6750.
∴当每件售价定为55元时,每星期的销售利润最大,最大利润为6750元.
(3)根据题意得:-30x2+3300x-84000≥6000,
解得:50≤x≤60.
答:为了使每星期利润不少于6000元,每件销售价x的取值范围为50≤x≤60.
点评 本题考查了二次函数的应用、二次函数的性质以及解一元二次不等式,解题的关键是:(1)根据数量关系总利润=(每件售价-40)×销售数量找出y关于x的函数表达式;(2)根据二次函数的性质解决最值问题;(3)结合(1)找出关于x的一元二次不等式.

练习册系列答案
相关题目
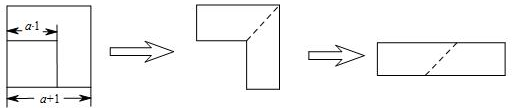
9.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1)剩余部分虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )cm2

| A. | 2 | B. | 2a | C. | 4a | D. | (a2-1) |
8.△ABC的外心在三角形的内部,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判断 |
9.下列命题中,属于假命题的是( )
| A. | 对顶角相等 | |
| B. | 三角形内角和等于180° | |
| C. | 全等三角形对应角相等 | |
| D. | 有三个角分别对应相等的两个三角形全等 |
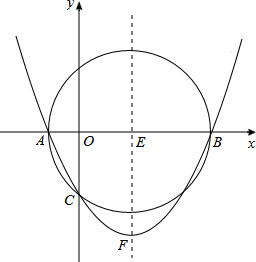 如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.
如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.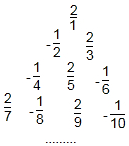 将分数:$\frac{2}{1}$,-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{1}{4}$,$\frac{2}{5}$,-$\frac{1}{6}$,$\frac{2}{7}$,-$\frac{1}{8}$,$\frac{2}{9}$,….将这列数排成如图形式:
将分数:$\frac{2}{1}$,-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{1}{4}$,$\frac{2}{5}$,-$\frac{1}{6}$,$\frac{2}{7}$,-$\frac{1}{8}$,$\frac{2}{9}$,….将这列数排成如图形式: 如图,已知∠ADE=∠C,可得DE∥CB.
如图,已知∠ADE=∠C,可得DE∥CB.