Question

6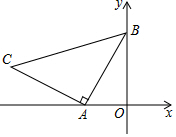．如图，等腰Rt△ABC，AB=AC，A（-1，0），B（0，4），则C点坐标为（-5，1）．

Answer 1

分析 先根据AAS判定△ACD≌△BAO，得出CD=AO，AD=BO，再根据点A的坐标为（-1，0），点B的坐标为（0，4），求得CD和OD的长，得出点C的坐标．

解答 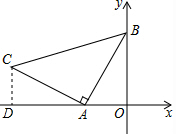解：过C作CD⊥x轴于D，则∠CDA=∠AOB=90°，
∵△ABC是等腰直角三角形，
∴∠CAB=90°，
又∵∠AOB=90°，
∴∠CAD+∠BAO=90°，∠ABO+∠BAO=90°，
∴∠CAD=∠ABO，
在△ACD和△BAO中，
$\left\{\begin{array}{l}{∠CDA=∠AOB}\\{∠CAD=∠ABO}\\{AC=BA}\end{array}\right.$，
∴△ACD≌△BAO（AAS），
∴CD=AO，AD=BO，
又∵点A的坐标为（-1，0），点B的坐标为（0，4），
∴CD=AO=1，AD=BO=4，
∴DO=5，
又∵点C在第三象限，
∴点C的坐标为（-5，1）．
故答案为：（-5，1）．

点评 本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，解决问题的关键是根据全等三角形的性质，求得点C到坐标轴的距离．