题目内容
如图,△ABC中,∠ABC=900,以AB为直径的⊙O交AC于D.E为弧AD上一点,连结AE,BE,BE交AC于点F,且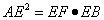
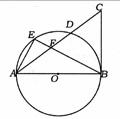
(1)求证:E是弧AD的中点。
(2)求证:CB=CF
(3)若点E到弦AD的距离为1,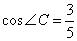 ,求⊙O的半径。
,求⊙O的半径。
【解析】(1)∵∠E=∠E ,AE2=EF·EB,∴ △ABC∽△ABC∴ ∠EAD=∠EBA ,即: 
∴ E是弧AD的中点;
(2)∵AB为⊙O的直径,∴ ∠E=900,∴ ∠CFB=∠EFA=900-∠EAD,∵ ∠ABC=900,∴ ∠CBF=900-∠EBA,又∵ ∠EAD=∠EBA,∴ ∠CFB=∠CBF,∴ CB=CF;
(3)连接OE交AC于点G,设⊙O的半径是x.
|

练习册系列答案
相关题目

 的顶点均在格点上,其中点
的顶点均在格点上,其中点 ,将
,将 逆时针旋转
逆时针旋转 后得到
后得到 .
.
 所经过的路径长为________;
所经过的路径长为________; 扫过的图形的面积之和.
扫过的图形的面积之和. B.
B.
 D.
D.

 B
B .
. C.
C. D.
D.
 ECD都是等腰直角三角形,
ECD都是等腰直角三角形,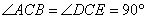 ,
,
 ,
,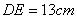 ,求
,求 的长.
的长.