题目内容
 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论:①BD⊥AC;②AD=DE;③BC=2AD;④∠AED=∠ACB.其中正确的是
如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论:①BD⊥AC;②AD=DE;③BC=2AD;④∠AED=∠ACB.其中正确的是考点:圆周角定理,相似三角形的判定与性质
专题:
分析:由在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,根据直径所对的圆周角是直角,可得①BD⊥AC;由圆的内接四边形,可得∠A=∠C=∠AED,即可得②AD=DE;④∠AED=∠ACB.
解答:解:①∵BC为直径,
∴∠BDC=90°,
∴BD⊥AC,
故正确;
②∴∠ADB=∠CDB=90°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠A=∠C,
∵∠AED=∠C=180°-∠BED,
∴∠A=∠AED,
∴AD=DE,
故正确;
③∵∠DBC不一定是30°,
∴BC不一定等于CD,
即BC不一定等于AD,
故错误;
④由③可得∠A=∠ACB,故正确.
故答案为:①②④.
∴∠BDC=90°,
∴BD⊥AC,
故正确;
②∴∠ADB=∠CDB=90°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠A=∠C,
∵∠AED=∠C=180°-∠BED,
∴∠A=∠AED,
∴AD=DE,
故正确;
③∵∠DBC不一定是30°,
∴BC不一定等于CD,
即BC不一定等于AD,
故错误;
④由③可得∠A=∠ACB,故正确.
故答案为:①②④.
点评:此题考查了圆周角定理、圆的内接四边形的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
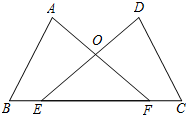 已知:如图,点E,F在BC上,BF=CE,∠A=∠D,∠B=∠C,AF与DE交于点O.试说明:
已知:如图,点E,F在BC上,BF=CE,∠A=∠D,∠B=∠C,AF与DE交于点O.试说明: 如图,等边△ABC,AD⊥BC,交BC于点D,BD=5cm,则AC的长为
如图,等边△ABC,AD⊥BC,交BC于点D,BD=5cm,则AC的长为