题目内容
11．
如图，在⊙O的内接五边形ABCDE中，∠B+∠E=222°，则∠CAD=42°．
分析 连接CE，根据圆内接四边形对角互补可得∠B+∠AEC=180°，进而求出∠CED的度数，再根据同弧所对的圆周角相等可得∠CED=∠CAD即可．
解答 解：如图，连接CE，
∵五边形ABCDE是圆内接五边形，
∴四边形ABCE是圆内接四边形，
∴∠B+∠AEC=180°，
∵∠B+∠AED=222°，
∴∠CED=42°，
∴∠CAD=∠CED=42°，
故答案为：42．
点评 本题考查了圆内接四边形的性质，同弧所对的圆周角相等的性质，熟记性质并作辅助线构造出圆内接四边形是解题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
20．
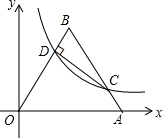如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y=$\frac{k}{x}$上（k＞0，x＞0），则k的值为（ ）
如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y=$\frac{k}{x}$上（k＞0，x＞0），则k的值为（ ）| A． | 25$\sqrt{3}$ | B． | 18$\sqrt{3}$ | C． | 9$\sqrt{3}$ | D． | 9 |
春节期间，某购物中心购进了一批3D气球进行销售，并特别推出了3D气球艺术展，让每一位顾客来感受浓浓的童真萌趣，根据市场调查，这种3D气球在一段时间内的销售量y（个）与销售单价（元/个）之间的对应关系如图所示．
如图，AB为⊙O的直径，点C、D在⊙O上．若∠CAB=40°，则∠D的大小为50度．
6．将多项式（x2-1）2+6（1-x2）+9因式分解，正确的是（ ）
| A． | （x-2）4 | B． | （x2-2）2 | C． | （x2-4）2 | D． | （x+2）2（x-2）2 |
16．下列各图中，可围成一个正方体的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，在⊙O中，AC∥OB，∠ABO=20°，则∠BOC的度数为40°．
如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为4.8cm．