题目内容
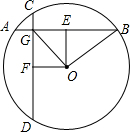 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为G,OE⊥AB,OF⊥CD,垂足分别为E,F,连接OG,OB.
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为G,OE⊥AB,OF⊥CD,垂足分别为E,F,连接OG,OB.(1)求证:四边形OEGF是正方形;
(2)若OB=5cm,OG=3
| 2 |
考点:垂径定理,勾股定理
专题:
分析:(1)先根据AB=CD,OE⊥AB,OF⊥CD可知OE=OF,∠OEG=∠OFG,再由AB⊥CD可知∠EGF=90°,故可得出结论;
(2)由(1)知四边形OEGF是正方形,故OE=GE,再由OG=3
cm可得出OE的长,根据勾股定理求出BE的长,进而可得出结论.
(2)由(1)知四边形OEGF是正方形,故OE=GE,再由OG=3
| 2 |
解答:(1)证明:∵AB=CD,OE⊥AB,OF⊥CD,
∴OE=OF,∠OEG=∠OFG=90°,
∵AB⊥CD,
∴∠EGF=90°,
∴四边形OEGF是正方形;
(2)解:∵由(1)知四边形OEGF是正方形,
∴OE=GE,
∵OG=3
cm,
∴2OE2=OG2,即2OE2=(3
)2,解得OE=3cm.
在Rt△OBE中,BE=
=
=4cm,
∴AB=2BE=8cm.
∴OE=OF,∠OEG=∠OFG=90°,
∵AB⊥CD,
∴∠EGF=90°,
∴四边形OEGF是正方形;
(2)解:∵由(1)知四边形OEGF是正方形,
∴OE=GE,
∵OG=3
| 2 |
∴2OE2=OG2,即2OE2=(3
| 2 |
在Rt△OBE中,BE=
| OB2-OE2 |
| 52-32 |
∴AB=2BE=8cm.
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,D是AC的中点,DE⊥AB于点E.求证:BC2=BE2-AE2.
如图,在△ABC中,∠C=90°,D是AC的中点,DE⊥AB于点E.求证:BC2=BE2-AE2. 如图,已知线段AB=2BC,DA=AB,M是线段AD的中点,N是线段AC的中点,试确定MN与AB+NB的大小关系.
如图,已知线段AB=2BC,DA=AB,M是线段AD的中点,N是线段AC的中点,试确定MN与AB+NB的大小关系.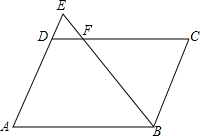 平行四边形ABCD的面积是30cm2,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大9cm2,且AD=5cm,那么DE等于多少cm?
平行四边形ABCD的面积是30cm2,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大9cm2,且AD=5cm,那么DE等于多少cm? 如图,在△ABC中,AB=AC=BC,高AD=h,求AB.
如图,在△ABC中,AB=AC=BC,高AD=h,求AB.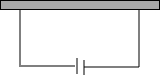 如图,要建一个面积为130m2的养鸡场,鸡场的一边靠墙(墙长16m),并在与墙平行一边开一道1m宽的门,现有32m长的木板.
如图,要建一个面积为130m2的养鸡场,鸡场的一边靠墙(墙长16m),并在与墙平行一边开一道1m宽的门,现有32m长的木板. 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?