题目内容
16. 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.(1)求证:AC是⊙O的切线;
(2)若BC=6,tan∠A=$\frac{3}{4}$,求CD的长.
分析 (1)连接DO,由等腰三角形的性质和角平分线的定义得出∠ODB=∠CBD,证出DO∥BC,由平行线的性质得出∠ADO=90°,即可得出结论;
(2)在Rt△ABC中,∠ACB=90°,根据三角函数的定义得到AC=8,根据相似三角形的性质得到R=$\frac{15}{4}$,在Rt△ABC中,根据三角函数的定义即可得到结论.
解答  (1)证明:如图,连接OD,
(1)证明:如图,连接OD,
∵⊙O经过B,D两点,
∴OB=OD,
∴∠OBD=∠ODB,
又∵BD是∠ABC的平分线,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∵∠ACB=90°,即BC⊥AC,
∴OD⊥AC.又OD是⊙O的半径,
∴AC是⊙O的切线;
(2)解:在Rt△ABC中,∠ACB=90°,
∵BC=6,tan∠BAC=$\frac{BC}{AC}=\frac{3}{4}$,
∴AC=8,
∵OD∥BC,
∴△AOD∽△ABC,
∴$\frac{OD}{BC}=\frac{OA}{AB}$,即$\frac{R}{6}=\frac{10-R}{10}$,
解得:R=$\frac{15}{4}$,
∴OD=$\frac{15}{4}$,
在Rt△ABC中,OD⊥AC,
∴tan∠A=$\frac{OD}{AD}=\frac{3}{4}$,
∴AD=5,
∴CD=3.
点评 本题考查了切线的判定、等腰三角形的性质、平行线的判定与性质、相似三角形的判定与性质、垂径定理等知识;本题综合性强,有一定难度,特别是(2)中,需要证明相似三角形求出半径才能得出结果.

练习册系列答案
相关题目
6.在某次体育测试中,九年级三班6位同学的立定跳远成绩(单位:米)分别为1.85,1.71,2.10,1.85,1.96,2.31.则这组数据的众数与极差分别是( )
| A. | 1.85和0.21 | B. | 2.10和0.46 | C. | 1.85和0.60 | D. | 2.31和0.60 |
7. 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )| A. | y=$\frac{1}{4}$(x+3)2 | B. | y=$\frac{1}{4}$(x-3)2 | C. | y=-$\frac{1}{4}$(x+3)2 | D. | y=-$\frac{1}{4}$(x-3)2 |
8.一元一次不等式x+1≥2的解在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
 如图,桌子上放着一个长方体的茶叶盒和一个圆柱形的水杯,则它的俯视图是( )
如图,桌子上放着一个长方体的茶叶盒和一个圆柱形的水杯,则它的俯视图是( )



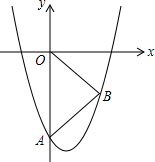 如图,抛物线y=x2-2x-6与y轴交于点A,点B是抛物线上一点,且在第四象限上,△ABO是以OA为底的等腰三角形,则∠AOB=45度.
如图,抛物线y=x2-2x-6与y轴交于点A,点B是抛物线上一点,且在第四象限上,△ABO是以OA为底的等腰三角形,则∠AOB=45度. 如图,在?ABCD中,E、F为对角线AC上两点,且DE∥BF,求证:△AFB≌△CED.
如图,在?ABCD中,E、F为对角线AC上两点,且DE∥BF,求证:△AFB≌△CED.