题目内容
11.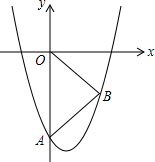 如图,抛物线y=x2-2x-6与y轴交于点A,点B是抛物线上一点,且在第四象限上,△ABO是以OA为底的等腰三角形,则∠AOB=45度.
如图,抛物线y=x2-2x-6与y轴交于点A,点B是抛物线上一点,且在第四象限上,△ABO是以OA为底的等腰三角形,则∠AOB=45度.
分析 作BD⊥y轴于D,根据等腰三角形的性质得出OD=AD,进而根据O、A的坐标求得D的坐标,即可求得B的纵坐标,代入解析式求得B的坐标,从而得出OD=BD,所以△OBD是等腰直角三角形,那么∠AOB=45°.
解答  解:如图,作BD⊥y轴于D,
解:如图,作BD⊥y轴于D,
∵△ABO是以OA为底的等腰三角形,
∴OD=AD,
∵抛物线y=x2-2x-6与y轴交于点A,
∴A(0,-6),
∵O(0,0),
∴OA=6,
∴OD=AD=3,
∴D(0,-3),
把y=-3代入y=x2-2x-6得,-3=x2-2x-6,
解得x=-1或3,
∴B(3,-3),
∴OD=BD=3,
∵BD⊥y轴,
∴△OBD是等腰直角三角形,
∴∠AOB=45°.
故答案为45.
点评 本题考查了等腰三角形的性质,二次函数图象上点的坐标特征,等腰直角三角形的判定与性质,求得B点的纵坐标是关键.

练习册系列答案
相关题目
2.在某次体育测试中,某小组8位同学的成绩分别是66,67,78,78,79,79,79,80,则这8人体育成绩的众数是( )
| A. | 77 | B. | 78 | C. | 78.5 | D. | 79 |
19.2015年河南省参加高考的考生数量为772325人,比2014年增加了4.8万人,将数据772325精确到千位用科学记数法表示为( )
| A. | 77.23×104 | B. | 7.72×105 | C. | 7.7×105 | D. | 77.2×104 |
20. 如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
 如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )
如图,直线a∥b,∠l=55°,∠2=45°,则∠3的度数为( )| A. | 110° | B. | 100° | C. | 90° | D. | 80° |
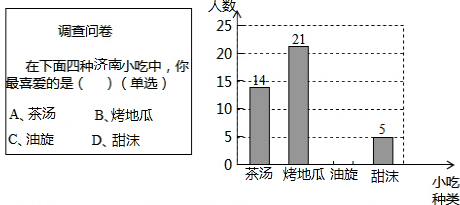
 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过(-3,0),对称轴直线为x=-1,给出四个结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过(-3,0),对称轴直线为x=-1,给出四个结论: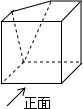 如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )
如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )