题目内容
6.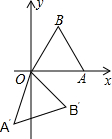 如图,等边三角形OAB的顶点O在坐标原点,顶点A在x轴上,OA=2,将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置,则点B′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
如图,等边三角形OAB的顶点O在坐标原点,顶点A在x轴上,OA=2,将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置,则点B′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
分析 过B作BE⊥OA于E,则∠BEO=90°,根据等边求出OB=OA=2,∠BOA=60°,根据旋转得出∠AOA′=105°,∠A′OB′=∠AOB=60°,求出∠AOB′=45°,解直角三角形求出B′E和OE即可.
解答 解: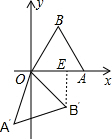
过B作BE⊥OA于E,则∠BEO=90°,
∵△OAB是等边三角形,A(2,0),
∴OB=OA=2,∠BOA=60°,
∵等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置,旋转角为105°,
∴∠AOA′=105°,∠A′OB′=∠AOB=60°,OB=OB′=2,
∴∠AOB′=105°-60°=45°,
在Rt△B′EO中,B′E=OE=$\frac{\sqrt{2}}{2}$OB′=$\sqrt{2}$,
即点B′的坐标为($\sqrt{2}$,-$\sqrt{2}$),
故答案为:($\sqrt{2}$,-$\sqrt{2}$).
点评 本题考查了等边三角形的性质,旋转的性质,解直角三角形的应用,能构造直角三角形是解此题的关键.

练习册系列答案
相关题目
11.今年学校运动会参加的人数是m人,比去年增加10%,那么去年运动会参加的人数为( )人.
| A. | (1+10%)m | B. | (1-10%)m | C. | $\frac{m}{1+10%}$ | D. | $\frac{m}{1-10%}$ |
 如图,△ABC与△BAD中,AD与BC相交于点M,∠1=∠2,∠C=∠D,试说明△ABC≌△BAD.请你在横线上添加一个条件,使得它可以用“AAS”来说明△ABC≌△BAD,并写出说理过程.
如图,△ABC与△BAD中,AD与BC相交于点M,∠1=∠2,∠C=∠D,试说明△ABC≌△BAD.请你在横线上添加一个条件,使得它可以用“AAS”来说明△ABC≌△BAD,并写出说理过程. 、
、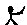 ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a b=a和a
b=a和a b=b.例如
b=b.例如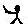 2=3,3
2=3,3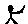 2=2,则(2015
2=2,则(2015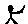 2016)
2016)