题目内容
11.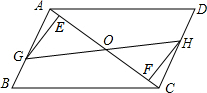 已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.(1)求证:EG∥FH;
(2)GH、EF互相平分.
分析 (1)由平行四边形的性质得到对边平行,得到内错角相等,根据三角形全等,得到边相等,角相等,再由邻补角得到内错角相等,得到两线平行;
(2)根据平行四边形的性质和判定得到结论.
解答 (1)证明:在?ABCD中,
∵AB∥CD,
∴∠GAE=∠HCF,
∵AF=CE,
∴AF-EF=CE=EF,
即;AE=CF,
在△AGE与△CHF中,
$\left\{\begin{array}{l}{AG=CH}\\{∠GAE=∠HCF}\\{AE=CF}\end{array}\right.$,
∴△AGE≌△CHF,
∴GE=HF,∠AEG=∠CFH,
∴∠GEO=∠HFO,
∴EG∥FH;
(2)由(1)证得GE=HF,EG∥FH,
∴四边形GFHE是平行四边形,
∴GH、EF互相平分.
点评 本题考查了平行四边形的性质和判定,全等三角形的判定与性质,注意数形结合,分清平行四边形的性质和判定.

练习册系列答案
相关题目
19.在Rt△ABC中,∠C=Rt∠,若BC:AC=3:4,BD平分∠ABC交AC于点D,则tan∠DBC的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
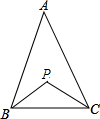 如图,在△ABC中,BP、CP分别为∠B、∠C的平分线,请探究∠A和∠P之间存在怎样的数量关系?说说你的理由.
如图,在△ABC中,BP、CP分别为∠B、∠C的平分线,请探究∠A和∠P之间存在怎样的数量关系?说说你的理由. 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.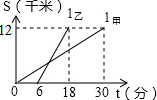 甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.
甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.