题目内容
19.在Rt△ABC中,∠C=Rt∠,若BC:AC=3:4,BD平分∠ABC交AC于点D,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 作DE⊥AB于E,设BC为3x,则AC为4x,求出AB=5x,设CD为a,根据勾股定理,用x表示a,根据三角函数的概念求出tan∠DBC的值.
解答 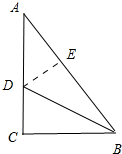 解:作DE⊥AB于E,
解:作DE⊥AB于E,
在Rt△ABC中,设BC为3x,则AC为4x,
根据勾股定理,AB=5x,
设CD为a,
BD平分∠ABC,则DE=CD=a,
AD=4x-a,AE=5x-3x=2x,
在Rt△ADE中,
AD2=DE2+AE2,
即(4x-a)2=a2+(2x)2,
解得,a=$\frac{3}{2}$x,
tan∠DBC=$\frac{1}{2}$
故选:B.
点评 本题考查的是解直角三角形和角平分线的知识,掌握锐角三角函数的概念、理解角平分线的性质是解题的关键,正确作出辅助线构造直角三角形是重要环节.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
14.下列各数中,整数部分为3的数是( )
| A. | π | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
11.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 正五边形 | C. | 菱形 | D. | 平行四边形 |
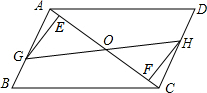 已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.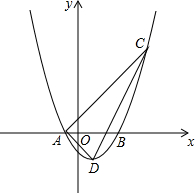 如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).
如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).