题目内容
16.若$\sqrt{(5-x)^{2}}$=x-5,$\sqrt{(x-10)^{2}}$=10-x,化简|3-x|-$\sqrt{(x-12)^{2}}$.分析 利用二次根式的性质得出x的取值范围,进而化简得出即可.
解答 解:∵$\sqrt{(5-x)^{2}}$=x-5,$\sqrt{(x-10)^{2}}$=10-x,
∴x-5≥0,10-x≥0,
解得:5≤x≤10,
∴|3-x|-$\sqrt{(x-12)^{2}}$
=x-3+(x-12)
=2x-15.
点评 此题主要考查了二次根式的性质与化简,正确化简二次根式是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
6. 实数a在数轴上的位置如图所示,则下列说法正确的是( )
实数a在数轴上的位置如图所示,则下列说法正确的是( )
 实数a在数轴上的位置如图所示,则下列说法正确的是( )
实数a在数轴上的位置如图所示,则下列说法正确的是( )| A. | a的相反数是2 | B. | a的倒数等于2 | C. | a的绝对值是2 | D. | a的绝对值大于2 |
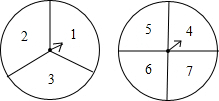 两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.
两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.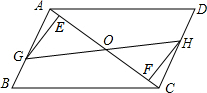 已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
已知:如图,在?ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.