题目内容
 已知:AD、BE是Rt△ABC的中线,∠ACB=90°,AD=
已知:AD、BE是Rt△ABC的中线,∠ACB=90°,AD=| 10 |
| 5 |
考点:勾股定理
专题:
分析:设AC=x,BC=y,根据三角形中线的定义可得CE=
x,CD=
y,然后利用勾股定理列式整理求出x2+y2,再利用勾股定理解答即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设AC=x,BC=y,
∵AD、BE是Rt△ABC的中线,
∴CE=
x,CD=
y,
在Rt△ACD中,CD2+AC2=AD2,
所以,
y2+x2=10,
在Rt△BCE中,BC2+CE2=BE2,
所以,y2+
x2=5,
所以,x2+y2=12,
在Rt△ABC中,由勾股定理得,AB=
=
=2
.
∵AD、BE是Rt△ABC的中线,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ACD中,CD2+AC2=AD2,
所以,
| 1 |
| 4 |
在Rt△BCE中,BC2+CE2=BE2,
所以,y2+
| 1 |
| 4 |
所以,x2+y2=12,
在Rt△ABC中,由勾股定理得,AB=
| AC2+BC2 |
| 12 |
| 3 |
点评:本题考查了勾股定理,三角形的中线的定义,是基础题,熟记定理并准确识图,利用勾股定理列出等式是解题的关键.

练习册系列答案
相关题目
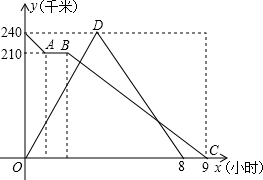 在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题﹕
在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题﹕ 如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.
如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.