题目内容
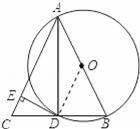
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O的半径为5,∠BAC=60°,求DE的长.


【考点】切线的判定;圆周角定理.
【专题】计算题;证明题.
【分析】(1)根据垂直平分线的判断方法与性质易得AD是BC的垂直平分线,故可得AB=AC;
(2)连接OD,由平行线的性质,易得OD⊥DE,且DE过圆周上一点D故DE为⊙O的切线;
(3)由AB=AC,∠BAC=60°知△ABC是等边三角形,根据等边三角形的性质,可得AB=BC=10,CD=
 BC=5;又∠C=60°,借助三角函数的定义,可得答案.
BC=5;又∠C=60°,借助三角函数的定义,可得答案.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°;
∵BD=CD,
∴AD是BC的垂直平分线.
∴AB=AC.
(2)证明:连接OD,
∵点O、D分别是AB、BC的中点,
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
∴DE为⊙O的切线.
(3)解:由AB=AC,∠BAC=60°知△ABC是等边三角形,
∵⊙O的半径为5,
∴AB=BC=10,CD=
 BC=5.
BC=5.
∵∠C=60°,
∴DE=CD•sin60°=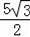
 .
.

【点评】本题考查切线的判定,线段相等的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

 )﹣1﹣|
)﹣1﹣|
 ﹣8|+2cos60°.
﹣8|+2cos60°. ,
, ,π,
,π, ,0.
,0. 中无理数的个数是( )
中无理数的个数是( )