题目内容
 如图,点P是正方形ABCD的BC边上一动点,PE⊥BD于E,PF⊥AC于F,若AC=12,则PE+PF的值是( )
如图,点P是正方形ABCD的BC边上一动点,PE⊥BD于E,PF⊥AC于F,若AC=12,则PE+PF的值是( )| A、6 | ||
| B、10 | ||
C、6
| ||
| D、12 |
考点:正方形的性质
专题:
分析:根据正方形的对角线互相垂直可得OB⊥OC,对角线平分一组对角可得∠OBC=45°,然后求出四边形OEPF为矩形,△BEP是等腰直角三角形,再根据矩形的对边相等可得PF=OE,根据等腰直角三角形的性质可得PE=BE,从而得到PE+PF=OB,然后根据正方形的性质解答即可.
解答:解:在正方形ABCD中,OB⊥OC,∠OBC=45°,
∵PE⊥BD,PF⊥AC,
∴四边形OEPF为矩形,△BEP是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OB,
∵AC=BC,
∴OB=
AC=6,
∴PE+PF=6,
故选A.
∵PE⊥BD,PF⊥AC,
∴四边形OEPF为矩形,△BEP是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OB,
∵AC=BC,
∴OB=
| 1 |
| 2 |
∴PE+PF=6,
故选A.
点评:考查了正方形的性质,矩形的判定与性质,等腰直角三角形的判定与性质,熟记各性质求出PE+PF=OB是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
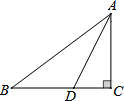 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )| A、3:4 | B、3:5 |
| C、4:5 | D、1:1 |
某服装的进价为每套120元,标价为每套200元,现在打折销售,为了不亏本,最多打( )
| A、八折 | B、七五折 | C、七折 | D、六折 |
 如图,直线l1:y=x+1与直线l2:y=mx-n相交于点P(1,2),则关于x、y的二元一次方程组
如图,直线l1:y=x+1与直线l2:y=mx-n相交于点P(1,2),则关于x、y的二元一次方程组 如图,点D、E在BC上,且△ABE≌△ACD,对于结论①AB=AC,②∠BAE=∠CAD,③BE=CD,④AD=DE,其中正确的个数是( )个.
如图,点D、E在BC上,且△ABE≌△ACD,对于结论①AB=AC,②∠BAE=∠CAD,③BE=CD,④AD=DE,其中正确的个数是( )个.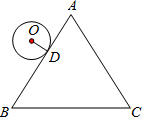 如图,等边△ABC的周长为8π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
如图,等边△ABC的周长为8π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( ) 如图,在△ABC和△ADE中,
如图,在△ABC和△ADE中,