题目内容
18.如图,下列图案均是长度相同的火柴并按一定的规律拼接而成:第1个图案需7根火柴,第2个图案需13根火柴,第3个图案需21根火柴,…,依此规律,第8个图案需火柴( )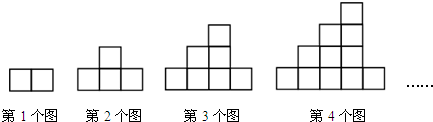
| A. | 90根 | B. | 91根 | C. | 92根 | D. | 93根 |
分析 根据第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,得出规律第n个图案需n(n+3)+3根火柴,再把8代入即可求出答案.
解答 解:第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…
第n个图案需n(n+3)+3根火柴,
则第8个图案需:8×(8+3)+3=91(根);
故选:B.
点评 此题主要考查了图形的变化类,关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,再利用规律解决问题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9. 如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
 如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )| A. | 33° | B. | 34° | C. | 43° | D. | 57° |
6.已知a+b=3,ab=2,则a2+b2=( )
| A. | 4 | B. | 6 | C. | 3 | D. | 5 |
13. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )| A. | 14 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
10.下列定理中逆定理不存在的是( )
| A. | 全等三角形的对应角相等 | |
| B. | 如果在一个三角形中,两边相等,那么它们所对的角也相等 | |
| C. | 同位角相等,两直线平行 | |
| D. | 角平分线上的点到这个角的两边的距离相等 |
7.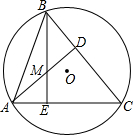 如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
 如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 6 |
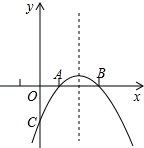 已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).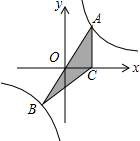 如图,已知经过原点的直线AB与反比例函数y=$\frac{k}{x}$(k≠0)图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为( )
如图,已知经过原点的直线AB与反比例函数y=$\frac{k}{x}$(k≠0)图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为( )