��Ŀ����
6��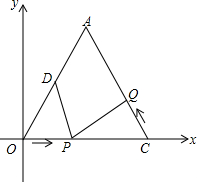 ��ֱ֪��y1=2$\sqrt{21}$x��ֱ��y2=-2$\sqrt{21}$x+16$\sqrt{21}$�ཻ���A��ֱ��y2��x�ύ�ڵ�C��DΪOA�е㣮
��ֱ֪��y1=2$\sqrt{21}$x��ֱ��y2=-2$\sqrt{21}$x+16$\sqrt{21}$�ཻ���A��ֱ��y2��x�ύ�ڵ�C��DΪOA�е㣮��1�������P���߶�OC����3����ÿ����ٶ���O����C���˶���ͬʱ��Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���OPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��OPD���CQPȫ�ȣ�
��2������Q��?���е��˶��ٶ��ɵ�C��������P��ԭ�����ٶȴӵ�Oͬʱ����������ʱ���ء�OCA�����˶������ʱ���P���Q��һ���ڡ�OCA����������������
���� ��1���������OP=CQ=3���ף����ɵ�C��ֱ��y2��x�ύ�㣬�������C�����꣬�����߶�OC�ij��ȣ��Ӷ����CP�ij��ȣ��������A�����꣬����A��OC���ϵĸߣ����ɵõ�������AOC�ǵ��������Σ��ɵá�DOP=��PCQ�������ù��ɶ��������OA�ij��ȣ���ΪDΪOA�е㣬�����OD�ij��ȣ������������н��Ƿ��Ӧ��ȼ����ж�������Ϊ��Q���˶��ٶ����P���˶��ٶȲ���ȣ�����OP��CQ���֡�DOP=��PCQ��Ҫʹ��OPD���CQPȫ�ȣ�ֻ��0P=CP=4���ף�����ȫ�ȵó�CQ=OD=2$\sqrt{85}$���ף�Ȼ������˶��ٶ�����˶�ʱ�䣬����ʱ���CQ�ij��������Q���˶��ٶȣ�
��2���辭��x���P���Q��һ������������·��������з��̣�������ɵ�ʱ�䣬����������ʱ����õ�P��·�̼��ɵõ����ڵıߣ�
��� �⣺��1���١߾���1�룬
��OP=CQ=3���ף�
��ͼ������A��AB��x�ᴹ��Ϊ
�ߵ�C��ֱ��y2��x�ύ�㣬
����y=0������y2=-2$\sqrt{21}$x+16$\sqrt{21}$�ã�
-2$\sqrt{21}$x+16$\sqrt{21}$=0
��ã�x=8��
���C��������8��0����
��OC=8���ף�
�ߵ�A��ֱ��y1=2$\sqrt{21}$x��ֱ��y2=-2$\sqrt{21}$x+16$\sqrt{21}$����
��$\left\{\begin{array}{l}{{y}_{1=}2\sqrt{21}x}\\{{y}_{2}=-2\sqrt{21}x+16\sqrt{21}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=4}\\{y=8\sqrt{21}}\end{array}\right.$
���A��������4��8$\sqrt{21}$����
��OB=BC=4���ף�
��AB��ֱƽ��OC��
��OA=CA��
���DOP=��PCQ��
����Rt��OAB�У�OA=$\sqrt{{OB}^{2}{+AB}^{2}}$=$\sqrt{{4}^{2}{+��8\sqrt{21}��}^{2}}$=4$\sqrt{85}$���ף�
��DΪOA�е㣬
��OD=2$\sqrt{85}$���ף�
�֡�OC=8���ף�OP=CQ=3���ף�
��CP=5���ף�
���OPD���CQP��
OP=CQ=3���ף���DOP=��PCQ��CP��OD��
���OPD���CQP��ȫ�ȣ�
�ڡߵ�Q���˶��ٶ����P���˶��ٶȲ���ȣ�
��OP��CQ��
�֡ߡ�DOP=��PCQ��
����ʹ��OPD���CQPȫ�ȣ�ֻ��OP=CP=4����
�ߡ�OPD�ա�CPQ��
��CQ=OD=2$\sqrt{85}$���ף�
���P���˶�ʱ��t=$\frac{4}{3}$�룬
���Q���˶��ٶ�Ϊ2$\sqrt{85}$��$\frac{4}{3}$=$\frac{3\sqrt{85}}{2}$������/�룩��
�൱��Q���˶��ٶ�Ϊ$\frac{3\sqrt{85}}{2}$����/��ʱ���ܹ�ʹ��OPD���CQPȫ�ȣ�
��2��������Q��?���е��˶��ٶ��ɵ�C��������P��ԭ�����ٶȴӵ�Oͬʱ����������ʱ���ء�OCA�����˶�������x�룬��P���Q��һ���ڡ�OCA�ı���������
����������з��̣�
$\frac{3\sqrt{85}}{2}$x=3x+8$\sqrt{85}$
��ã�x=$\frac{1360+32\sqrt{85}}{243}$��
���P���˶�·��Ϊ��$\frac{1360+32\sqrt{85}}{243}$��3=$\frac{1360+32\sqrt{85}}{81}$���ף�
��OC+CA=8+4$\sqrt{85}$��44��9���ף�$\frac{1360+32\sqrt{85}}{81}$���ס�20.4���ף�
��OC����P���˶�·�̣�OC+CA��
��Ӧ�ڱ�CA�ϵ�һ��������
������Q��?���е��˶��ٶ��ɵ�C��������P��ԭ�����ٶȴӵ�Oͬʱ����������ʱ���ء�OCA�����˶�������$\frac{1360+32\sqrt{85}}{243}$�룬��P���Q��һ���ڡ�OCA�ı�AC��������
���� ������Ҫ����һ�κ����Ľ��㣬��������Ľ��������֪ʶ��������ȫ�ȵ��ж������ʣ����������ε����ʣ��Լ����ν��˼������ã�ͨ��������꣬����߶εij����ǽ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
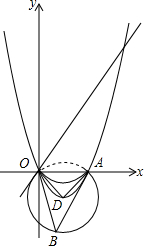 ��ͼ��֪����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx-8k��ͼ����x�ύ�ڵ�A��������y=ax2+bx��a��0������O��A���㣮
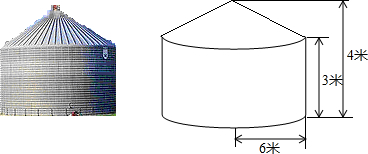
��ͼ��֪����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx-8k��ͼ����x�ύ�ڵ�A��������y=ax2+bx��a��0������O��A���㣮 ��ͼ����֪Բ��ĸ�߳�Ϊ6������չ��ͼ�����Σ��������12�У������Բ����չ��ͼ�л�AC�ij�����4�У�
��ͼ����֪Բ��ĸ�߳�Ϊ6������չ��ͼ�����Σ��������12�У������Բ����չ��ͼ�л�AC�ij�����4�У�