题目内容
15.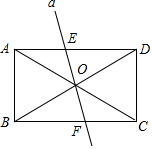 在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,
在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,(1)若CF=2,BC比CD大3,求BF的长度.
(2)若∠DBC=30°,直线α沿射线ED的方向平移.设△OBF的面积为S1,直线α在四边形OFCD中扫过的面积为S2,x=S2:S1,求x的范围;
(3)在(1)的条件下,若M、N分别在线段BO、BF上的动点,直接写出FM+MN的最小值是$\frac{3}{2}$.
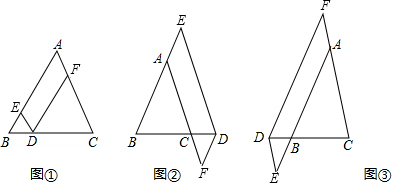
分析 (1)如图1中,连接DF,设CD=x,则BC=x+3.首先证明DF=BF=x+1,在Rt△DFC中,利用勾股定理构建方程即可解决问题;
(2)如图2中,连接DF.利用相似三角形的性质求出,$\frac{{S}_{△BOF}}{{S}_{四边形ODCF}}$=$\frac{1}{2}$的值,即可解决问题;
(3)如图3中,连接EM,作EH⊥BC于H,交BD于K.易证BD垂直平分EF,推出ME=MF,推出MF+MN=EM+MN,根据垂线段最短可知,当M与K重合,N与H重合时,MF+MN的值最小,最小值为EH;
解答 解:(1)如图1中,连接DF,设CD=x,则BC=x+3.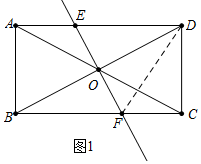
∵CF=2,
∴BF=BC-CF=x+1,
∵四边形ABCD是矩形,
∴OB=OD,∵EF⊥BD,
∴BF=DF=x+1.
在Rt△DFC中,∵DF2=CD2+CF2,
∴(x+1)2=x2+22,
∴x=$\frac{3}{2}$,
∴BF=x+1=$\frac{5}{2}$.
(2)如图2中,连接DF.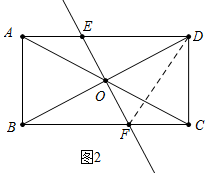
∵四边形ABCD是矩形,
∴OD=OC,∠BCD=90°,
∵∠OBC=30°,
∴∠ODC=60°,
∴△ODC是等边三角形,设CD=OD=OC=OB=a,则BC=$\sqrt{3}$a,
∴∠OBF=∠CBD,∠BOF=∠BCD,
∴△BOF∽△BCD,
∴$\frac{{S}_{△BOF}}{{S}_{△BCD}}$=($\frac{OB}{BC}$)2=$\frac{1}{3}$,
∴$\frac{{S}_{△BOF}}{{S}_{四边形ODCF}}$=$\frac{1}{2}$,
∴$\frac{{S}_{2}}{{S}_{1}}$是最大值为2,
∴0<x≤2.
(3)如图3中,连接EM,作EH⊥BC于H,交BD于K.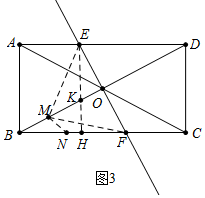
易证BD垂直平分EF,∴ME=MF,
∴MF+MN=EM+MN,
根据垂线段最短可知,当M与K重合,N与H重合时,MF+MN的值最小,最小值为EH,
∵四边形ABHE是矩形,
∴EH=AB=$\frac{3}{2}$,
∴MF+MN的最小值为$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查几何变换综合题、矩形的性质、相似三角形的判定和性质、勾股定理、垂线段最短等知识,解题的关键是学会构建方程解决问题,学会利用对称,根据垂线段最短解决最短问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案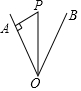 如图,点P在∠AOB的平分线上,PA⊥OA于A,若PA=3,则点P到OB的距离为( )
如图,点P在∠AOB的平分线上,PA⊥OA于A,若PA=3,则点P到OB的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图是一个几何体的三视图,其中俯视图是等边三角形
如图是一个几何体的三视图,其中俯视图是等边三角形