题目内容
2. 如图所示:四边形ABCD是平行四边形,DE平分∠ADC,BF平分∠ABC.试证明∠E=∠F.
如图所示:四边形ABCD是平行四边形,DE平分∠ADC,BF平分∠ABC.试证明∠E=∠F.
分析 由四边形ABCD是平行四边形,可证得AB∥CD,∠ADC=∠ABC,AD∥BC,又由DE平分∠ADC,BF平分∠ABC,易证得四边形BEDF是平行四边形,即可判定∠E=∠F.
解答  证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADC=∠ABC,AD∥BC,
∴∠2=∠5,
∵DE平分∠ADC,BF平分∠ABC,
∴∠2=$\frac{1}{2}$∠ADC,∠4=$\frac{1}{2}$∠ABC,
∴∠2=∠4,
∴∠4=∠5,
∴DE∥BF,
∴四边形BEDF是平行四边形,
∴∠E=∠F.
点评 此题考查了平行四边形的性质与判定.注意证得四边形BEDF是平行四边形是关键.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a5+a3=a8 | C. | a5÷a5=1(a≠0) | D. | (a3)2=a5 |
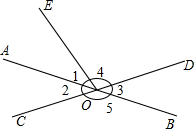 如图:直线AB、CD交与点O,∠1=∠2.
如图:直线AB、CD交与点O,∠1=∠2.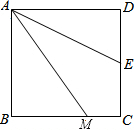 【问题情境】
【问题情境】 如图,已知点P是射线ON上一动点(可在射线ON上运动),∠AON=35°,设∠OAP=x度,当x满足0<x<55或90<x<145条件时,△AOP为钝角三角形.
如图,已知点P是射线ON上一动点(可在射线ON上运动),∠AON=35°,设∠OAP=x度,当x满足0<x<55或90<x<145条件时,△AOP为钝角三角形.