题目内容
在Rt△ABC中,a、b、c分别为∠A、∠B、∠C的对边,∠C=90°,a=12,cosA=
,求b、c及∠B的值.
| 4 |
| 5 |
考点:解直角三角形
专题:
分析:根据cosA=
可以求得b和c的大小关系,再根据a=12即可求得b、c的值,即可解题.
| 4 |
| 5 |
解答:解:∵cosA=
,
∴b=
c,
∵a2+b2=c2,
代入a=12得:c=20,b=16,
∵cosA=
,
∴sinB=
,
∴∠B=53.13°.
| 4 |
| 5 |
∴b=
| 4 |
| 5 |
∵a2+b2=c2,
代入a=12得:c=20,b=16,
∵cosA=
| 4 |
| 5 |
∴sinB=
| 4 |
| 5 |
∴∠B=53.13°.
点评:本题考查了勾股定理的运用,考查了正弦、余弦值的计算,本题中根据勾股定理求得b、c的值是解题的关键.

练习册系列答案
相关题目
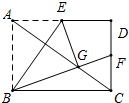 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.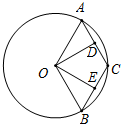 如图,C是
如图,C是
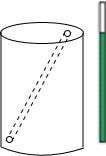 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)