题目内容
13.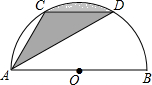 如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.
如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.(1)当CD∥AB时,图中阴影部分的面积为$\frac{8}{3}$πcm2;
(2)当C,D在半圆上运动时,阴影部分的最大面积为$\frac{8}{3}$π+4$\sqrt{3}$cm2.
分析 (1)连接OC、OD,根据已知条件可得∠COD=60°,△OCD是等边三角形,将阴影部分的面积转化为扇形OCD的面积求解即可;
(2)利用图形可得出当C,D有一个点与A或B重合时此时阴影部分面积最大,进而求出即可.
解答 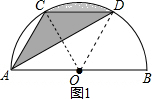 解:(1)如图1,连接OC、OD.
解:(1)如图1,连接OC、OD.
∵弧$\widehat{CD}$的度数为60°,
∴∠COD=60°,
∵OC=OD,
∴△OCD是等边三角形,CD=OC=$\frac{1}{2}$AB=8cm.
∵CD∥AB,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}$π(cm2);
故答案是:$\frac{8}{3}$π
(2)如图2,当C,D有一个点与A或B重合时此时阴影部分面积最大,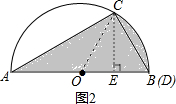
连接CO,过点C作CE⊥AB于点E,
∵AB=8,∴AO=CO=4,
∵$\widehat{CD}$的度数为60°,
∴∠CAD=30°,∠COE=60°,
∴EO=2,则EC=2$\sqrt{3}$,
∴阴影部分的最大面积为:$\frac{1}{2}$AO×EC+S扇形COB=$\frac{1}{2}$×4×2$\sqrt{3}$+$\frac{60π×{4}^{2}}{360}$=4$\sqrt{3}$+$\frac{8π}{3}$.
故答案是:$\frac{8}{3}$π+4$\sqrt{3}$
点评 本题考查了扇形面积的计算,判断出△OCD与△CDA是等底等高的三角形,且△OCD是等边三角形,利用扇形的面积公式求解是解题关键.

练习册系列答案
相关题目

 如图,若PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,则AB与CD平行吗?为什么?
如图,若PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,则AB与CD平行吗?为什么?
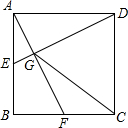 如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2.
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2.