题目内容
抛物线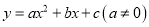 上部分点的横坐标
上部分点的横坐标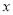 ,纵坐标y的对应值如下表:
,纵坐标y的对应值如下表:
| … | -3 | -2 | -1 | 0 | 1 | … |
| … | -6 | 0 | 4 | 6 | 6 | … |
容易看出,(-2,0)是它与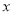 轴的一个交点,那么它与
轴的一个交点,那么它与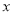 轴的另一个交点的坐标为 .
轴的另一个交点的坐标为 .
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
题目内容
抛物线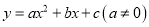 上部分点的横坐标
上部分点的横坐标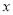 ,纵坐标y的对应值如下表:
,纵坐标y的对应值如下表:
| … | -3 | -2 | -1 | 0 | 1 | … |
| … | -6 | 0 | 4 | 6 | 6 | … |
容易看出,(-2,0)是它与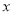 轴的一个交点,那么它与
轴的一个交点,那么它与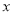 轴的另一个交点的坐标为 .
轴的另一个交点的坐标为 .
 智能训练练测考系列答案
智能训练练测考系列答案