题目内容
20.若b为实数,化简|2b-1|-$\sqrt{{b}^{2}-2b+1}$.分析 分b≤$\frac{1}{2}$、$\frac{1}{2}$≤b≤1、b≥1三种情况,根据二次根式的性质把原式进行化简即可.
解答 解:原式=|2b-1|-|b-1|,
当b≤$\frac{1}{2}$时,原式=-2b+1+b-1=-b,
当$\frac{1}{2}$≤b≤1时,原式=2b-1+b-1=3b-2,
当b≥1时,原式=2b-1-b+1=b.
点评 本题考查的是二次根式的化简,从不同的范围对原式进行化简是解题的关键,解答时,先对b的取值范围进行确定,然后根据$\sqrt{{a}^{2}}$=|a|进行化简.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.2014年在进入12月份后又迎来了大幅降温提拿起,12月5日哈尔滨、沈阳、石家庄、济南的最高气温分别为-12°、17°、6°、5°,则这四个城市中在这天的最高气温最高的是( )
| A. | 哈尔滨 | B. | 沈阳 | C. | 石家庄 | D. | 济南 |
12.函数y=$\sqrt{1-x}$的自变量x的取值范围是( )
| A. | x>1 | B. | x<1 | C. | x≤1 | D. | x≥1 |
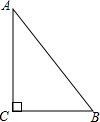 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°. 如图,AC是菱形ABCD的对角线,若∠BAC=50°,则∠ADB等于40°.
如图,AC是菱形ABCD的对角线,若∠BAC=50°,则∠ADB等于40°.