题目内容
(1)探究规律:
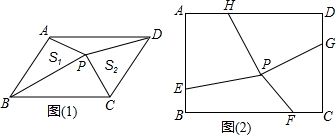
已知:如图(1),点P为?ABCD内一点,△PAB、△PCD的面积分别记为S1、S2,□ABCD 的面积记为S,试探究S1+S2与S之间的关系.
(2)解决问题:
如图(2)矩形ABCD中,AB=6,BC=9,点E、F、G、H分别在AB、BC、CD、DA上,且AE=CG=4,AH=CF=3.点P为矩形内一点,四边形AEPH、四边形CGPF的面积分别记为S1、S2,求S1+S2.
已知:如图(1),点P为?ABCD内一点,△PAB、△PCD的面积分别记为S1、S2,□ABCD 的面积记为S,试探究S1+S2与S之间的关系.

(2)解决问题:
如图(2)矩形ABCD中,AB=6,BC=9,点E、F、G、H分别在AB、BC、CD、DA上,且AE=CG=4,AH=CF=3.点P为矩形内一点,四边形AEPH、四边形CGPF的面积分别记为S1、S2,求S1+S2.
考点:矩形的性质,平行四边形的性质
专题:
分析:(1)过P点做一条平行AB的直线EF,可得S1的面积是平行四边形ABEF的一半,S2是平行四边形EFDC的一半,继而可得出S1+S2=
S.
(2)连接EF、FG、GH、HE,证出四边形EFGH为平行四边形,求得四边形EFGH的面积,△HEP的面积+△GPF的面积=?EFGH面积的一半,再用S1+S2=△HEP的面积+△GPF的面积+△AEH的面积+△GFC的面积求解.
| 1 |
| 2 |
(2)连接EF、FG、GH、HE,证出四边形EFGH为平行四边形,求得四边形EFGH的面积,△HEP的面积+△GPF的面积=?EFGH面积的一半,再用S1+S2=△HEP的面积+△GPF的面积+△AEH的面积+△GFC的面积求解.
解答: 答:(1)S1+S2=
答:(1)S1+S2=
S.
证明:如图(1),过P点做EF∥AB,
∵AB∥CD,
∴EF∥CD,
则S1=
S?ABEF,S2=
S?EFDC,
∵S?ABEF+S?EFDC=S,
∴S1+S2=
S.
(2)如图(2),连接EF、FG、GH、HE,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,
∵AE=CG,AH=CF,
在△AEH和△CGF中,
,
∴△AEH和△CGF(SAS),
∴HE=FG,
同理得HG=FE,
∵AB=6,BC=9,AE=CG=4,AH=CF=3,
∴BE=AB-AE=6-4=2,BF=BC-CF=9-3=6,DG=CD-CG=6-4=2,HD=AD-AH=9-3=6,
∴△HEP的面积+△GPF的面积
=?EFGH面积的一半
=(矩形ABCD-4个三角形的面积)÷2
=(6×9-
×4×3-
×4×3-
×2×6-
×2×6)÷2
=15,
∴S1+S2=△HEP的面积+△GPF的面积+△AEH的面积+△GFC的面积
=15+
×4×3+
×4×3
=27.
 答:(1)S1+S2=
答:(1)S1+S2=| 1 |
| 2 |
证明:如图(1),过P点做EF∥AB,
∵AB∥CD,
∴EF∥CD,
则S1=
| 1 |
| 2 |
| 1 |
| 2 |
∵S?ABEF+S?EFDC=S,
∴S1+S2=
| 1 |
| 2 |
(2)如图(2),连接EF、FG、GH、HE,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,
∵AE=CG,AH=CF,
在△AEH和△CGF中,
|
∴△AEH和△CGF(SAS),
∴HE=FG,
同理得HG=FE,
∵AB=6,BC=9,AE=CG=4,AH=CF=3,
∴BE=AB-AE=6-4=2,BF=BC-CF=9-3=6,DG=CD-CG=6-4=2,HD=AD-AH=9-3=6,
∴△HEP的面积+△GPF的面积
=?EFGH面积的一半
=(矩形ABCD-4个三角形的面积)÷2
=(6×9-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=15,
∴S1+S2=△HEP的面积+△GPF的面积+△AEH的面积+△GFC的面积
=15+
| 1 |
| 2 |
| 1 |
| 2 |
=27.
点评:考查了平行四边形的性质,解答本题的关键是掌握平行四边形对边平行的性质.同时考查了矩形的性质及全等三角形的判定及性质,注意面积的转化.

练习册系列答案
相关题目
不等式6x<4x-1的解集是( )
A、x>
| ||
B、x>-
| ||
C、x<-
| ||
D、x<
|
 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
 某物体的三视图如图:则此物体的全面积等于
某物体的三视图如图:则此物体的全面积等于