题目内容
3.已知|a|=$\frac{3}{7}$,|b|=$\frac{9}{20}$,且b<a,试求ab的值.分析 根据绝对值的意义得到a=±$\frac{3}{7}$,b=±$\frac{9}{20}$,由于b<a,则a=$\frac{3}{7}$时,b=-$\frac{9}{20}$;a=-$\frac{3}{7}$时,b=-$\frac{9}{20}$,然后把a、b的值分别代入ab中计算即可.
解答 解:∵|a|=$\frac{3}{7}$,|b|=$\frac{9}{20}$,
∴a=±$\frac{3}{7}$,b=±$\frac{9}{20}$,
而b<a,
∴a=$\frac{3}{7}$时,b=-$\frac{9}{20}$;a=-$\frac{3}{7}$时,b=-$\frac{9}{20}$,
∴ab=±$\frac{27}{140}$.
点评 本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=-a.也考查了有理数的加减法和乘法.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
14.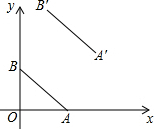 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )| A. | (2,6) | B. | (2,5) | C. | (6,2) | D. | (3,6) |