题目内容
13.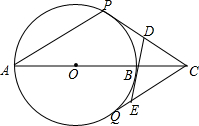 如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )| A. | 4 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 连接PO,PB.首先证明∠OCP=30°,由此求出PC,再证明△DEC的周长=2PC即可解决问题.
解答 解:如图,连接PO,PB.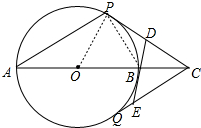
∵CP、CQ是切线,
∴CP=CQ,OP⊥CP,
∴∠CPO=90°,
∵OB=BC=OP,
∴OC=2OP,
∴∠OC=30°,∵OP=3,
∴OC=6,PC=$\sqrt{O{C}^{2}-O{P}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∵DP、DB是切线,
∴DB=DP,
∵EB、EQ是切线,
∴EB=EQ,
∴△EDC的周长=CE+BE+BD+CD=CE+EQ+CD+DP=CQ+CP=2CP=6$\sqrt{3}$,
故选D.
点评 本题可知切线的性质、直角三角形30度角的判定,切线长定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1. 如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
 如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
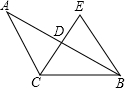 如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.
如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形. 如图是2015年11月的日历.
如图是2015年11月的日历. 画出旋转后的图形:如图,将点A绕点O旋转60°(逆时针)
画出旋转后的图形:如图,将点A绕点O旋转60°(逆时针)