题目内容
3.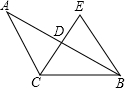 如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.
如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.
分析 根据CE⊥AB于点D,且DE=DC得出BC=BE,根据角的关系得出∠ECB=60°,即可证得△CEB为等边三角形.
解答 证明:∵CE⊥AB于点D,且DE=DC,
∴BC=BE,
∵AC=BC,∠ACB=120°,CE⊥AB于点D,
∴∠ECB=60°,
∴△CEB为等边三角形.
点评 本题考查了等边三角形的判定,等腰三角形的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
8.下列各数中,比-1小1的数为( )
| A. | 0 | B. | 1 | C. | -2 | D. | 2 |
15. 如图,AB∥CD,若∠C=30°,则∠B的度数是( )
如图,AB∥CD,若∠C=30°,则∠B的度数是( )
 如图,AB∥CD,若∠C=30°,则∠B的度数是( )
如图,AB∥CD,若∠C=30°,则∠B的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
13.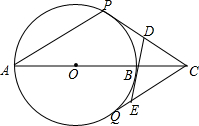 如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
 如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )| A. | 4 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |