题目内容
6.方程方程x2=x的解是x1=0,x2=1;2-$\sqrt{3}$的倒数是2+$\sqrt{3}$;分解因式:x2-9=(x+3)(x-3).分析 将方程化为一般形式,提取公因式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;根据倒数的定义进行填空;利用平方差公式进行因式分解.
解答 解:x2=x,
移项得:x2-x=0,
分解因式得:x(x-1)=0,
可得x=0或x-1=0,
解得:x1=0,x2=1.
2-$\sqrt{3}$的倒数是:$\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2+$\sqrt{3}$.
x2-9=(x+3)(x-3).
故答案为:x1=0,x2=1;2+$\sqrt{3}$;(x+3)(x-3).
点评 此题考查了解一元二次方程-因式分解法,利用此方法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.

练习册系列答案
相关题目
18.2015年的世界无烟日期间,小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中20个成年人吸烟,对于这个关于数据收集与处理的问题,下列说法正确的是( )
| A. | 调查的方式是普查 | B. | 本地区约有20%的成年人吸烟 | ||
| C. | 样本是20个吸烟的成年人 | D. | 本地区只有80个成年人不吸烟 |
15.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a2+2ab-b2=(a-b)2 | C. | (a3)2=a6 | D. | ab2+a2b=a3b2 |
 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4)、B(-2,1)、C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4)、B(-2,1)、C(-5,2).
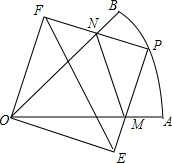 如图,在半径为1的扇形AOB中∠AOB=45°,P为弧AB上一动点(不与A,B重合),以OP为对角线作正方形OEPF,分别交OA,OB于M,N,给出以下结论:
如图,在半径为1的扇形AOB中∠AOB=45°,P为弧AB上一动点(不与A,B重合),以OP为对角线作正方形OEPF,分别交OA,OB于M,N,给出以下结论: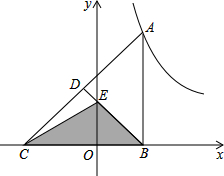 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$3\sqrt{6}$,则k的值为6$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$3\sqrt{6}$,则k的值为6$\sqrt{6}$.